1 Introduction
1.1 Context and objectives
The geometrical characterization of granular media (grains, pores, fibers, etc.) is an important issue in materials and process sciences. Indeed, several granular media can be modeled as random sets where the heterogeneity of the particles is studied with a probabilistic approach [12, 24]. In this context, the random closed sets (RACSs) have been particularly studied [29, 21, 8, 2] to get geometrical characteristics of such granular media. A RACS denotes a random variable defined on a probability space $(\varOmega ,\mathfrak{A},P)$ valued in $(\mathbb{F},\mathfrak{F})$, the family of closed subsets of ${\mathbb{R}}^{d}$ provided with the σ-algebra $\mathfrak{F}:=\sigma \{\{F\in \mathbb{F}\hspace{2.5pt}|F\cap X\ne \varnothing \}\hspace{0.1667em}X\in \mathfrak{K}\}$, where $\mathfrak{K}$ denotes the class of compact subsets on ${\mathbb{R}}^{d}$. In a probabilistic point of view, the distribution of a convex RACS is uniquely determined from the Choquet capacity functional [23, 16]. However, such a description is not suitable for explicitly determining the geometrical shape of the RACS. An alternative way is to describe a RACS by the probability distribution of real-valued geometrical characteristics (area, perimeter, diameters, etc.).
1.2 Original contribution
The aim of this paper is to show how such characteristics can be used to describe the geometrical shape of a convex random closed set in ${\mathbb{R}}^{2}$. It has already been shown [25] that the moments of the Feret diameter of a convex random closed set in ${\mathbb{R}}^{2}$ can be obtained by the area measures on morphological transforms of it. A Feret diameter (also known as caliper diameter) is a measure of a set size along a specified direction. It can be defined as the distance between the two parallel planes restricting the set perpendicular to that direction.
A set $X\in {\mathbb{R}}^{2}$ is said to be central symmetric or, more simply, symmetric if it is equal to the set $\breve{X}:=-X$. Note that the Feret diameter is not sensitive to such a central symmetrization [22]. Indeed, for a nonempty compact convex set $X\subset {\mathbb{R}}^{2}$, its symmetrized set $\frac{1}{2}(X\oplus \breve{X})$ (see [21, 17]) has the same Feret diameter as X. Consequently, the Feret diameter of a convex set X is not enough to fully reconstruct X (but only its symmetrized set). However, the Feret diameter is still useful to describe the shape of convex sets for two reasons. Firstly, a convex set X and its symmetrized set $\frac{1}{2}(X\oplus \breve{X})$ share a lot of common geometrical descriptors (perimeter, eccentricity, etc.). Secondly, there are many applications in which symmetric convex particles are considered. In this way, the reported work is focused on the symmetric convex sets (i.e., $X=\frac{1}{2}(X\oplus \breve{X})$). By abusing the notation, the conditions “nonempty and compact” will be often omitted in this paper. In other words, without explicit mentioning of the contrary, a convex set will refer to a nonempty compact convex set.
In this paper, we show that the Feret diameter of a random symmetric convex set can be used to define some approximations of it as random zonotopes. The polygonal approximation of a deterministic convex set has already been studied several times [18, 14, 4, 7]. However, in most cases, the approximation is made by using the support function, which is not available in most of the geometric stochastic models. Random polygons have already been studied several times [10, 3, 20]. However, they are defined in different ways and for other objectives, and they are not characterized from their Feret diameters. In our point of view, a zonotope (which is a Minkowski sum of line segments) is described by its faces (direction and length) and can be characterized by its Feret diameter. We will show that the Feret diameter of a symmetric convex set evaluated on a finite number of directions $N>1$ can be used to define some approximations of it as zonotope. Such zonotope approximations will be generalized to the random symmetric convex sets. Therefore, a random symmetric convex set will be approximated by a random zonotope, and such approximations will be characterized from the Feret diameter of the random symmetric convex set. The considered random zonotope will be uniquely determined by the lengths of its faces, and their directions will be assumed to be known. The approximations considered are consistent as $N\to \infty $ with respect to the Hausdorff distance.
This work is a preliminary study in order to describe the geometrical characteristics of a population of convex particles in the context of image analysis. Indeed, such images of population of convex particles can be modeled by stochastic geometric models. In such a model, the projection of a particle represented by a random convex set. Consequently, this work can be used to get information on such convex particles. In addition, when the particles are supposed to be symmetric, they have a symmetric 2-D projection that can be fully characterized by the Feret diameter. Such a symmetric hypothesis is suitable in several industrial applications in chemical engineering (gas absorption, distillation, liquid–liquid extraction, petroleum processes, crystallization, etc.).
An area of application is the gas–liquid reactions. Indeed in a such process, the gas bubbles can be modeled as an ellipsoid the 2-D projections of which are ellipses (see [32, 30, 5]). The main area of application is crystals manufacturing. Indeed, many crystals are 3-D zonohedrons, and their 2-D projections are zonotopes. For example, the crystals of oxalate ammonium [26, 1], the crystals of calcium oxalate dihydrate [31], or the (L)-glutamic acid [6]. In such applications, the considered approximations coincide with the real data.
1.3 Outline of the paper
The paper is organized as follows. The first part is devoted to the case of a deterministic symmetric convex set X. Some properties of the Feret diameter are first recalled, and then for any integer $N>1$, an approximation ${X_{0}^{(N)}}$ of X as a zonotope [11] is described. It is shown that this approximation is consistent as $N\to \infty $ with respect to the Hausdorff distance [27]. A more accurate zonotope approximation ${\tilde{X}_{0}^{(N)}}$ of X that is invariant up to a rotation is also defined with the consistency also satisfied. This approximation is particularly interesting to describe the geometrical shape of X.
The second part is devoted to a characterization of the random zonotopes. First, we explore some properties of the random process associated with the Feret diameter. Then we study the random zonotopes, define some their classes, and discuss their descriptions by their faces. Finally, we study the characterization of some random zonotopes from their Feret diameters random process.
In the last part, we study a random symmetric convex set X. We show that it can still be described as precisely as we want by a random zonotope ${X_{0}^{(N)}}$ and up to a rotation by a random zonotope ${X_{\infty }^{(N)}}$ with respect to the Hausdorff distance. We give the properties of these approximates and show that they can be characterized from the Feret diameter random process of X. In particular, the mean and autocovariance of the Feret diameter random process of X can be used to get the mean and the variances of the random vectors composed by the face lengths of their zonotope approximations.
2 Description of a symmetric convex set as a zonotope from its Feret diameter
The aim of this section is to discuss how a convex set X can be described as a zonotope. We will show that X can always be approximated as precisely as we want by zonotopes and how such zonotopes can be characterized from the Feret diameter of X. First, we need to recall the definition of the Feret diameter and some its properties.
2.1 Feret diameter and the support function
Definition 1 (Support function).
Let $X\subset {\mathbb{R}}^{2}$ be a convex set. The support function of X is defined as
\[ f_{X}:\Bigg|\begin{array}{r@{\hskip10.0pt}c@{\hskip10.0pt}l}{\mathbb{R}}^{2}& \longrightarrow & \mathbb{R}\\{} x& \longmapsto & \sup _{s\in X}\langle x,s\rangle =\max _{s\in X}\langle x,s\rangle ,\end{array}\]
where $\langle \cdot ,\cdot \rangle $ denotes the Euclidean dot product.The support function allows us to fully characterize a convex set. Indeed, any positive homogeneous convex real-valued function on ${\mathbb{R}}^{2}$ is the support function of a convex set [27]. In the following, we give some important properties of the support function. The proofs are omitted since they can be found in the literature [13, 27].
Proposition 1 (Properties of the support function).
Let $X\subset {\mathbb{R}}^{2}$ be a convex set. Its support function satisfies the following properties:
-
1. Positive homogeneity: $\forall r\ge 0$, $f_{X}(rx)=rf_{X}(x)$.
-
2. Subadditivity: $f_{X}(x+y)\le f_{X}(x)+f_{X}(y)$.
-
3. $f_{X\oplus Y}=f_{X}+f_{Y}$, where ⊕ denotes the Minkowski addition.
-
4. If s is a vectorial similarity and $b\in {\mathbb{R}}^{2}$, then $f_{s(X)+b}(x)=f_{X}(s(x))+\langle x,b\rangle $.
-
6. If, in addition, $0\in X$, then $f_{X}\ge 0$.
-
7. $d_{H}(X,Y)=\| f_{X}-f_{Y}\| _{\infty }$, where $d_{H}$ denotes the Hausdorff distance, and $\| \cdot \| _{\infty }$ is the uniform norm on the unit sphere.
Items 1 and 2 relate the convexity of the support function, and expression (1) allows the reconstruction of a convex set from its support function. Note that the positive homogeneity of the support function involves that it can be completely determined on the Euclidean unit sphere. We adopt the following representation for the support function of X:
\[ h_{X}:\Bigg|\begin{array}{r@{\hskip10.0pt}c@{\hskip10.0pt}l}\mathbb{R}& \longrightarrow & \mathbb{R}\\{} \theta & \longmapsto & h_{X}(\theta )=f_{X}({}^{t}(-\sin (\theta ),\cos (\theta ))),\end{array}\]
which is a continuous and $2\pi $-periodic function.Note that the Feret diameter of a convex set X, denoted $H_{X}$, can be expressed by the support function as
where $\breve{X}$ is the usual notation for the symmetric set $-X$. It is easy to see that the Feret diameter of X coincides with the support function of $X\oplus \breve{X}$, where ⊕ denotes the Minkowski sum. Therefore, the functional $H_{X}$ is sufficient to fully characterize the symmetrized body $\frac{1}{2}(X\oplus \breve{X})$. Note that if X is already symmetric, then $H_{X}$ fully characterizes X. We recall some important properties of the Feret diameter.
(2)
\[ \forall \theta \in \mathbb{R},\hspace{1em}H_{X}(\theta )=h_{X}(\theta )+h_{\breve{X}}(\theta ),\]Proposition 2 (Properties of the Feret diameter).
Let X be a convex set. Then its Feret diameter $H_{X}$ satisfies the following properties:
-
1. For tow convex sets X and Y, $H_{X\oplus Y}=H_{X}+H_{Y}$.
-
2. $\forall r\in \mathbb{R}$, $H_{rX}=|r|H_{X}$.
-
3. If $R_{\eta }$ is a rotation and $b\in {\mathbb{R}}^{2}$, then $\forall \theta \in \mathbb{R}$, $H_{R_{\eta }(X)+b}(\theta )=H_{X}(\theta +\eta )$.
-
4. π- periodicity: $\forall \theta \in \mathbb{R}$, $H_{X}(\theta +\pi )=H_{X}(\theta )$.
-
5. For two symmetric bodies X and Y, $H_{X}\le H_{Y}\Leftrightarrow X\subseteq Y$
Proof.
$\hspace{0.2222em}$
□
-
4. The π-periodicity follows from $h_{\breve{X}}(\theta )=h_{X}(\theta +\pi )$, $\theta \in \mathbb{R}$.
-
5. Because of the symmetry of X and Y, if $H_{X}\le H_{Y}$, then $h_{X}\le h_{Y}$. Therefore, for any $x\in {\mathbb{R}}^{2}$, $f_{X}(x)\le f_{Y}(x)$, so $\{y\in {\mathbb{R}}^{2}|\langle y,x\rangle \le f_{X}(x)\}\subseteq \{y\in {\mathbb{R}}^{2}|\langle y,x\rangle \le f_{Y}(x)\}$, and thus $X\subset Y$ by Proposition 1.5.Suppose that $X\subset Y$. Then $\forall x\in {\mathbb{R}}^{2}$, $\{\langle s,x\rangle |s\in X\}\subset \{\langle s,x\rangle |s\in Y\}\Rightarrow f_{X}(x)\le f_{Y}(x)\Rightarrow h_{X}\le h_{Y}\Rightarrow H_{X}\le H_{Y}$.
-
6. For any $(\theta ,\beta )\in {\mathbb{R}}^{2}$, let $\alpha =\beta +\pi $, $x={}^{t}(-\sin (\theta ),\cos (\theta ))$, $z={}^{t}(-\sin (\theta +\alpha ),\cos (\theta +\alpha ))$ and $y=z+x$, so that\[\begin{array}{r@{\hskip0pt}l}& \displaystyle f_{X}(y-x)\le f_{X}(-x)+f_{X}(y),\\{} & \displaystyle h_{X}(\theta +\alpha )\le h_{X}(\theta +\pi )+f_{X}(y),\end{array}\]and\[\begin{array}{r@{\hskip0pt}l}\displaystyle \parallel y\parallel & \displaystyle =\sqrt{{\big(\sin (\theta )+\sin (\theta +\alpha )\big)}^{2}+{\big(\cos (\theta )+\cos (\theta +\alpha )\big)}^{2}}\\{} & \displaystyle =\sqrt{(2+2\big(\sin (\theta )\sin (\theta +\alpha )+\cos (\theta )\cos (\theta +\alpha )\big)}\\{} & \displaystyle =\sqrt{2}\sqrt{1+\cos (\alpha )}\\{} & \displaystyle =\sqrt{2}\sqrt{2{\cos }^{2}\bigg(\frac{\alpha }{2}\bigg)}\\{} & \displaystyle =2\bigg|\cos \bigg(\frac{\alpha }{2}\bigg)\bigg|\\{} & \displaystyle =2\bigg|\sin \bigg(\frac{\beta }{2}\bigg)\bigg|.\end{array}\]Using the formulas\[\begin{array}{r@{\hskip0pt}l}\displaystyle \sin (\theta )+\sin (\theta +\alpha )& \displaystyle =2\sin \bigg(\theta +\frac{\alpha }{2}\bigg)\cos \bigg(\frac{\alpha }{2}\bigg),\\{} \displaystyle \cos (\theta )+\cos (\theta +\alpha )& \displaystyle =2\cos \bigg(\theta +\frac{\alpha }{2}\bigg)\cos \bigg(\frac{\alpha }{2}\bigg)\end{array}\]and taking $\eta \in \mathbb{R}$ such that $y=\parallel y\parallel {}^{t}(-\sin (\eta ),\cos (\eta ))$, we have\[\begin{array}{r@{\hskip0pt}l}\displaystyle \sin (\eta )& \displaystyle =\frac{2\sin (\theta +\frac{\alpha }{2})\cos (\frac{\alpha }{2})}{\parallel y\parallel },\\{} \displaystyle \cos (\eta )& \displaystyle =\frac{2\cos (\theta +\frac{\alpha }{2})\cos (\frac{\alpha }{2})}{\parallel y\parallel }.\end{array}\]Let s be the sign of $\cos (\frac{\alpha }{2})$. Then $\sin (\eta )=s\sin (\theta +\frac{\alpha }{2})$ and $\cos (\eta )=s\cos (\theta +\frac{\alpha }{2})$.Finally, $\eta \in \{\theta +\frac{\beta +\pi }{2},\theta +\frac{\beta +\pi }{2}+\pi \}$, and it can be expressed as\[ h_{X}(\theta +\beta -\pi )\le h_{X}(\theta +\pi )+2\bigg|\sin \bigg(\frac{\beta }{2}\bigg)\bigg|h_{X}(\eta ).\]This result is true for any convex set X, in particular, for $Y=\frac{1}{2}(X\oplus \breve{X})$. However, $h_{y}=H_{X}$, and then by the π-periodicity of the Feret diameter we have
The Feret diameter can also be related to the mixed area [27] by using a line segment as a structural element. Indeed, using the Steiner formula [27] with two convex sets X and Y, we have
where $W(X,Y)$ denotes the mixed area between X and Y. The mixed area functional $W(\cdot ,\cdot )$ is a symmetric mapping, which is also homogeneous in its two variables (see [19, 27] for details). It is often used to describe some morphological characteristics of a convex set X by using different structuring elements. For instance, if X is a bounded convex set and B is the unit disk, then $W(X,B)=\frac{1}{2}U(X)$, where $U(X)$ denotes the perimeter of X. Let X be a bounded convex set, and $S_{\theta }$ be a unit line segment directed by θ. Then
The proof is omitted since it consists in a simple drawing and can be found in the literature [25, 19].
Remark 1.
This relation is very important because it involves an interpretation of the mixed area of a convex set with the Minkowski addition of line segments from its Feret diameter. Indeed, for any $\theta _{1},\theta _{2}\in [0,\pi ]$ and $\alpha _{1},\alpha _{2}\in \mathbb{R}_{+}$,
Relation (5) has an important kind of linearity. Indeed, it implies formulae for the computation of the mixed area between a convex set and a symmetric body from their Feret diameter (see Remark Remark 3).
\[\begin{array}{r@{\hskip0pt}l}\displaystyle A(X\oplus \alpha _{1}S_{\theta _{1}}\oplus \alpha _{2}S_{\theta _{2}})& \displaystyle =A(X\oplus \alpha _{1}S_{\theta _{1}})+2W(X\oplus \alpha _{1}S_{\theta _{1}},\alpha _{2}S_{\theta _{2}})\\{} & \displaystyle =A(X)+\alpha _{1}H_{X}(\theta _{1})+\alpha _{2}H_{X\oplus \alpha _{1}S_{\theta _{1}}}(\theta _{2})\\{} & \displaystyle =A(X)+\alpha _{1}H_{X}(\theta _{1})+\alpha _{2}H_{X}(\theta _{2})+\alpha _{2}H_{\alpha _{1}S_{\theta _{1}}}(\theta _{2}).\end{array}\]
However, $\alpha _{2}H_{\alpha _{1}S_{\theta _{1}}}(\theta _{2})=W(\alpha _{1}S_{\theta _{1}},S_{\theta _{2}})=A(\alpha _{1}S_{\theta _{1}}\oplus \alpha _{2}S_{\theta _{2}})$. Then,
\[ W(X,\alpha _{1}S_{\theta _{1}}\oplus \alpha _{2}S_{\theta _{2}})=\frac{1}{2}\big(\alpha _{1}H_{X}(\theta _{1})+\alpha _{2}H_{X}(\theta _{2})\big).\]
This result can be easily generalized by induction to any Minkowski sum of line segments: $\forall n\ge 1$, $\forall i=1,\dots ,n$, $\alpha _{i}\in \mathbb{R}_{+},\theta _{i}\in \mathbb{R}$, we have
(5)
\[ W\Bigg(X,{\underset{i=1}{\overset{n}{\bigoplus }}}\alpha _{i}S_{\theta _{i}}\Bigg)=\frac{1}{2}{\sum \limits_{i=1}^{n}}\alpha _{i}H_{X}(\theta _{i}).\]2.2 Approximation of a symmetric convex set by a 0-regular zonotope
Now we give some properties of the Feret diameter of a convex set and its connection with the mixed area. Here the zonotope will be defined and particularly the class of the 0-regular zonotopes, some properties of the zonotopes will be discussed. In particular, we will show how a symmetric convex set can be approximated by a 0-regular zonotope as precisely as we want.
Let $\mathcal{C}$ denote the class of all symmetric convex sets of ${\mathbb{R}}^{2}$, where the symmetry is given in the sense of Minkowski: $X=\frac{1}{2}(X\oplus \breve{X})$. Let $S_{0}$ be the unit line segment $[-\frac{1}{2},\frac{1}{2}]$, and $S_{t}$ its rotation by the angle $t\in [0,\pi [$. Consider now the convex set X such that
Note that X is a compact convex symmetric polygon with at most $2n$ faces, where for all $i=1,\dots ,n$, $\alpha _{i}$ is the length of the two faces of X oriented by $\theta _{i}$. It is easy to see that every compact convex symmetric polygon has an even number of faces and can be represented as (6) up to a translation. Furthermore, note that X has a nonempty interior if and only if $n>1$.
(6)
\[ X={\underset{i=1}{\overset{n}{\bigoplus }}}\alpha _{i}S_{\theta _{i}},\hspace{1em}n\in {\mathbb{N}}^{\ast },\hspace{2.5pt}\forall i=1,\dots n,\hspace{2.5pt}\alpha _{i}\in \mathbb{R}_{+},\hspace{2.5pt}\theta _{i}\in [0,\pi [.\]Definition 2 (Zonotopes).
Any compact convex symmetric polygon such as (6) is called a zonotope. For $N\in {\mathbb{N}}^{\ast }$, ${\mathcal{C}}^{(N)}$ denotes the set of all zonotopes with at most $2N$ faces:
\[ {\mathcal{C}}^{(N)}=\Bigg\{{\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}S_{\theta _{i}}\big|\alpha \in {\mathbb{R}_{+}^{N}},\hspace{0.2778em}\theta \in [0,\pi {[}^{N}\Bigg\},\]
where $\alpha ={}^{t}(\alpha _{1},\dots \alpha _{N})$ and $\theta ={}^{t}(\theta _{1},\dots \theta _{N})$.Several geometric characteristics and properties of zonotopes can be easily expressed from representation (6).
Proposition 3 (Geometrical characterization of zonotopes).
Let $N\in {\mathbb{N}}^{\ast }$, and $X={\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}}$ be an element of ${\mathcal{C}}^{(N)}$. Let $H_{X}$ be its Feret diameter function, $U(X)$ its perimeter, and $A(X)$ its area. Then
Proof.
$\hspace{0.2222em}$
□
-
(6) For any $(\beta ,\eta )\in {\mathbb{R}}^{2}$, the support function of the line segment $S_{\beta }$ in the direction η is\[\begin{array}{r@{\hskip0pt}l}\displaystyle h_{S_{\beta }}(\eta )& \displaystyle =\underset{t\in [-\frac{1}{2},\frac{1}{2}]}{\max }\big\{t\big(-\cos (\beta )\sin (\eta )+\sin (\beta )\cos (\eta )\big)\big\}\\{} & \displaystyle =\underset{t\in [-\frac{1}{2},\frac{1}{2}]}{\max }\big\{t\sin (\beta -\eta )\big\}\\{} & \displaystyle =\frac{1}{2}\big|\sin (\beta -\eta )\big|\\{} \displaystyle \Rightarrow \hspace{1em}H_{S_{\beta }}(\eta )& \displaystyle =\big|\sin (\beta -\eta )\big|.\end{array}\]Then relation (7) follows from Propositions 2.1 and 2.2.
-
(7) If X is a polygon of $2N$ faces of length $\alpha _{i}$, $i=1,\dots ,N$, the perimeter can be obtained by adding up the face lengths.
-
(8) For the area, the result (9) is proved by induction on N: for $N=1$, $X=S_{\theta _{1}}$ and $A(X)=0$, so that (9) is satisfied. Suppose that (9) is true for $n\le N$ and let us show that it is true for $N+1$. Since $X=({\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}})\oplus \alpha _{N+1}S_{\theta _{N+1}}$, by the Steiner formula we have\[\begin{array}{r@{\hskip0pt}l}\displaystyle A(X)& \displaystyle =A\Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}S_{\theta _{i}}\Bigg)+2W\Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}S_{\theta _{i}},\alpha _{N+1}S_{\theta _{N+1}}\Bigg).\end{array}\]Then, by (4),\[ 2W\Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}S_{\theta _{i}},\alpha _{N+1}S_{\theta _{N+1}}\Bigg)=\alpha _{N+1}H_{{\textstyle\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}}}(\theta _{N+1}),\]and finally, by the heredity assumption and (7),\[\begin{array}{r@{\hskip0pt}l}\displaystyle A(X)& \displaystyle =\frac{1}{2}{\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}\alpha _{i}\alpha _{j}\big|\sin (\theta _{i}-\theta _{j})\big|+\alpha _{N+1}H_{{\textstyle\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}}}(\theta _{N+1})\\{} & \displaystyle =\frac{1}{2}{\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}\alpha _{i}\alpha _{j}\big|\sin (\theta _{i}-\theta _{j})\big|+\alpha _{N+1}{\sum \limits_{i=1}^{N}}\alpha _{i}\big|\sin (\theta _{N+1}-\theta _{i})\big|\\{} & \displaystyle =\frac{1}{2}{\sum \limits_{i=1}^{N+1}}{\sum \limits_{j=1}^{N+1}}\alpha _{i}\alpha _{j}\big|\sin (\theta _{i}-\theta _{j})\big|,\end{array}\]which proves (9).
In the following, we use a regular subdivision θ. We will show that if the subdivision step is sufficiently small, then any symmetric convex set can be approximated by a zonotope as precisely as we want.
Definition 3 (0-regular zonotopes).
For $N\in {\mathbb{N}}^{\ast }$, let ${\mathcal{C}_{0}^{(N)}}$ denote the class of all zonotopes with at most $2N$ faces oriented by the regular subdivision of $[0,\pi [$ by N elements:
Such zonotopes are called 0-regular zonotopes.
Note that ${\mathcal{C}_{0}^{(N)}}\subset {\mathcal{C}}^{(N)}$ and ${\mathcal{C}_{0}^{(N_{1})}}\subset {\mathcal{C}_{0}^{(N_{2})}}$ if and only if $N_{1}$ is a splitter of $N_{2}$. In addition, ${\mathcal{C}_{0}^{(N)}}$ can be identified to ${\mathbb{R}_{+}^{N}}$ by the mapping $\alpha \to X=({\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}})$, which is an isomorphism between the semigroups $({\mathbb{R}_{+}^{N}},+)$ and $({\mathcal{C}_{0}^{(N)}},\oplus )$. That is, this mapping is a bijection, and
\[ \forall \big(\alpha ,{\alpha ^{\prime }}\big)\in {\mathbb{R}_{+}^{N}}\times {\mathbb{R}_{+}^{N}},\hspace{1em}\Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}\big(\alpha _{i}+{\alpha ^{\prime }_{i}}\big)S_{\theta _{i}}\Bigg)=\Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}S_{\theta _{i}}\Bigg)\oplus \Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}{\alpha ^{\prime }_{i}}S_{\theta _{i}}\Bigg).\]
Theorem 1 (Approximation in ${\mathcal{C}_{0}^{(N)}}$).
Let $X\in \mathcal{C}$.
-
1. For all $N>1$, let ${F}^{(N)}$ denote the squared matrix $(|\sin (\theta _{i}-\theta _{j})|)_{1\le i,j\le N}$ and ${H_{X}^{(N)}}={}^{t}(H_{X}(\theta _{1}),\dots ,H_{X}(\theta _{N}))$. Thenbelongs to ${\mathcal{C}_{0}^{(N)}}$ and satisfies
(10)
\[ {X_{0}^{(N)}}={\underset{i=1}{\overset{N}{\bigoplus }}}\big({{F}^{(N)}}^{-1}{H_{X}^{(N)}}\big)_{i}S_{\theta _{i}}\]where $\operatorname{diam}(X)=\sup _{s\in \mathbb{R}}(H_{X}(s))$ denotes the maximal diameter of X and $d_{H}$ the Hausdorff distance.(11)
\[ \forall N>1,\hspace{1em}d_{H}\big(X,{X_{0}^{(N)}}\big)\le (6+2\sqrt{2})\sin \bigg(\frac{\pi }{2N}\bigg)\operatorname{diam}(X),\]Consequently, the sequence of 0-regular zonotopes $({X_{0}^{(N)}})_{N>1}$ approximates X in the following sense:We call ${X_{0}^{(N)}}$ the ${\mathcal{C}_{0}^{(N)}}$-approximation of X.(12)
\[ d_{H}\big(X,{X_{0}^{(N)}}\big)\longrightarrow 0\hspace{1em}\textit{as}\hspace{0.2778em}N\longrightarrow \infty .\]
Proof.
$\hspace{0.2222em}$
□
-
2. For integer $N>1$, it is easy to see that the matrix ${F}^{(N)}$ is invertible since ${F}^{(N)}$ is a circulant matrix [15] and its eigenvalues are exactly the coefficients of the discrete Fourier transform [28] of the signal $|\sin (\cdot )|$ (these coefficients are all strictly positive). Let $\alpha ={{F}^{(N)}}^{-1}{H_{X}^{(N)}}$ be such that Let us show that ${X_{0}^{(N)}}$ is the unique element of ${\mathcal{C}_{0}^{(N)}}$ satisfying $H_{{X_{0}^{(N)}}}(\theta _{i})=H_{X}(\theta _{i})$, $i=1,\dots ,N$. Suppose that there exists ${X^{\prime }}\in {\mathcal{C}_{0}^{(N)}}$ satisfying $H_{{X^{\prime }}}(\theta _{i})=H_{X}(\theta _{i})$, $i=1,\dots ,N$. Then ${X^{\prime }}$ can be written as ${X^{\prime }}={\bigoplus _{i=1}^{N}}{\alpha ^{\prime }_{i}}S_{\theta _{i}}$, and then ${H_{X}^{(N)}}={F}^{(N)}{\alpha ^{\prime }}$. The invertibility of ${F}^{(N)}$ implies $\alpha ={\alpha ^{\prime }}$, which means that ${X_{0}^{(N)}}={X^{\prime }}$.
-
1. Let us find an upper bound for the Hausdorff distance.For all $\eta \in \mathbb{R}$, there exists $i\in \{1,\dots ,N\}$ such that $\eta =\theta _{i}+\delta $ with $|\delta |\le \frac{\pi }{2N}$. Using inequality (3) with $\theta =\theta _{i}$ and $\beta =\delta $ for ${X_{0}^{(N)}}$, we have\[\begin{array}{r@{\hskip0pt}l}& \displaystyle H_{{X_{0}^{(N)}}}(\eta )\le H_{{X_{0}^{(N)}}}(\theta _{i})+2\bigg|\sin \bigg(\frac{\delta }{2}\bigg)\bigg|H_{{X_{0}^{(N)}}}\bigg(\theta _{i}+\frac{\delta +\pi }{2}\bigg).\end{array}\]Using inequality (3) with $\theta =\eta $ and $\beta =-\delta $ for X, we have\[\begin{array}{r@{\hskip0pt}l}& \displaystyle H_{X}(\theta _{i})\le H_{X}(\eta )+2\bigg|\sin \bigg(\frac{-\delta }{2}\bigg)\bigg|H_{X}\bigg(\theta _{i}+\frac{\delta +\pi }{2}\bigg)\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle -H_{X}(\eta )\le -H_{X}(\theta _{i})+2\bigg|\sin \bigg(\frac{\delta }{2}\bigg)\bigg|H_{X}\bigg(\theta _{i}+\frac{\delta +\pi }{2}\bigg).\end{array}\]Considering the equality $H_{{X_{0}^{(N)}}}(\theta _{i})=H_{X}(\theta _{i})$, from the two previous inequalities it follows that\[\begin{array}{r@{\hskip0pt}l}& \displaystyle H_{{X_{0}^{(N)}}}(\eta )\hspace{0.1667em}-\hspace{0.1667em}H_{X}(\eta )\hspace{0.1667em}\le \hspace{0.1667em}2\bigg|\sin \bigg(\frac{\delta }{2}\bigg)\bigg|\bigg(H_{X}\bigg(\theta _{i}\hspace{0.1667em}+\hspace{0.1667em}\frac{\delta +\pi }{2}\bigg)\hspace{0.1667em}+\hspace{0.1667em}H_{{X_{0}^{(N)}}}\bigg(\theta _{i}\hspace{0.1667em}+\hspace{0.1667em}\frac{\delta +\pi }{2}\bigg)\bigg).\end{array}\]In the same manner, using (3) with $\theta =\theta _{i}$ and $\beta =\delta $ for X and with $\theta =\eta $ and $\beta =-\delta $ for ${X_{0}^{(N)}}$, we have\[\begin{array}{r@{\hskip0pt}l}& \displaystyle H_{X}(\eta )\hspace{0.1667em}-\hspace{0.1667em}H_{{X_{0}^{(N)}}}(\eta )\hspace{0.1667em}\le \hspace{0.1667em}2\bigg|\sin \bigg(\frac{\delta }{2}\bigg)\bigg|\bigg(H_{X}\bigg(\theta _{i}\hspace{0.1667em}+\hspace{0.1667em}\frac{\delta +\pi }{2}\bigg)\hspace{0.1667em}+\hspace{0.1667em}H_{{X_{0}^{(N)}}}\bigg(\theta _{i}\hspace{0.1667em}+\hspace{0.1667em}\frac{\delta \hspace{0.1667em}+\hspace{0.1667em}\pi }{2}\bigg)\bigg).\end{array}\]Therefore, by denoting $\operatorname{diam}(X)=\sup _{\theta }\{H_{X}(\theta )\}$ and $\operatorname{diam}({X_{0}^{(N)}})=\sup _{\theta }\{H_{{X_{0}^{(N)}}}(\theta )\}$ it follows thatFurthermore,
(15)
\[ \big|H_{X}(\eta )-H_{{X_{0}^{(N)}}}(\eta )\big|\le 2\sin \bigg(\frac{\pi }{2N}\bigg)\big(\operatorname{diam}(X)+\operatorname{diam}\big({X_{0}^{(N)}}\big)\big).\]\[\begin{array}{r@{\hskip0pt}l}\displaystyle H_{{X_{0}^{(N)}}}(\eta )& \displaystyle ={\sum \limits_{j=1}^{N}}\alpha _{j}\big|\sin (\theta _{i}+\delta -\theta _{j})\big|\\{} & \displaystyle ={\sum \limits_{j=1}^{N}}\alpha _{j}\big|\sin (\theta _{i}-\theta _{j})\cos (\delta )-\cos (\theta _{i}-\theta _{j})\sin (\delta )\big|\\{} & \displaystyle \le \big|\cos (\delta )\big|{\sum \limits_{j=1}^{N}}\alpha _{j}\big|\sin (\theta _{i}-\theta _{j})\big|\hspace{0.1667em}+\hspace{0.1667em}\big|\sin (\delta )\big|{\sum \limits_{j=1}^{N}}\bigg|\sin \bigg(\theta _{i}-\theta _{j}+\frac{\pi }{2}\bigg)\bigg|\\{} & \displaystyle \le \big|\cos (\delta )\big|H_{{X_{0}^{(N)}}}(\theta _{i})+\big|\sin (\delta )\big|H_{{X_{0}^{(N)}}}\bigg(\frac{\pi }{2}\bigg)\\{} & \displaystyle \le \big|\cos (\delta )\big|H_{X}(\theta _{i})+\big|\sin (\delta )\big|\operatorname{diam}\big({X_{0}^{(N)}}\big)\\{} & \displaystyle \le \big|\cos (\delta )\big|\operatorname{diam}(X)+\big|\sin (\delta )\big|\operatorname{diam}\big({X_{0}^{(N)}}\big)\\{} & \displaystyle \le \operatorname{diam}(X)+\sin \bigg(\frac{\pi }{2N}\bigg)\operatorname{diam}\big({X_{0}^{(N)}}\big)\\{} \displaystyle \Rightarrow & \displaystyle \hspace{1em}\operatorname{diam}\big({X_{0}^{(N)}}\big)\bigg(1-\sin \bigg(\frac{\pi }{2N}\bigg)\bigg)\le \operatorname{diam}(X),\\{} \displaystyle N\ge 2\hspace{1em}\Rightarrow & \displaystyle \hspace{1em}\operatorname{diam}\big({X_{0}^{(N)}}\big)\le \frac{\sqrt{2}}{\sqrt{2}-1}\operatorname{diam}(X).\end{array}\]Then from (15) we have\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \big|H_{X}(\eta )-H_{{X_{0}^{(N)}}}(\eta )\big|\le 2\sin \bigg(\frac{\pi }{2N}\bigg)\bigg(1+\frac{\sqrt{2}}{\sqrt{2}-1}\bigg)\operatorname{diam}(X)\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle \underset{\eta }{\sup }\big|\big(H_{X}(\eta )-H_{{X_{0}^{(N)}}}(\eta )\big)\big|=d_{H}\big(X,{X_{0}^{(N)}}\big)\\{} & \displaystyle \hspace{1em}\le (6+2\sqrt{2})\sin \bigg(\frac{\pi }{2N}\bigg)\operatorname{diam}(X).\end{array}\]Consequently, $d_{H}(X,{X_{0}^{(N)}})\longrightarrow 0$ as $N\longrightarrow \infty $. -
3. Note that $Y_{N}={\bigcap _{i=1}^{N}}\{x\in {\mathbb{R}}^{2}$, $|\langle x,{}^{t}(-\sin (\theta _{i}),\cos (\theta _{i}))\rangle |\le \frac{1}{2}H_{X}(\theta _{i})\}$. Then $Y_{N}\in {\mathcal{C}_{0}^{(N)}}$. Indeed, each set of the intersection is the space between two lines oriented by one of the $\theta _{i}$; thus, $Y_{N}$ is a polygon with faces directed by the $\theta _{i}$, and therefore it belongs to ${\mathcal{C}_{0}^{(N)}}$. Because of the symmetry of X, it is easy to see that $X=\bigcap _{s\in [0,\pi ]}\{x\in {\mathbb{R}}^{2}$, $|\langle x,{}^{t}(-\sin (s),\cos (s))\rangle |\le \frac{1}{2}H_{X}(s)\}$; therefore, $X\subset Y_{N}$, and consequently $H_{X}\le H_{Y_{N}}$. Furthermore, because of the expression of $Y_{N}$ for any $i=1,\dots ,N$, $H_{X}(\theta _{i})\ge H_{Y_{N}}(\theta _{i})$ with the equality on $\theta _{i}$, and according to the foregoing, $Y_{N}={X_{0}^{(N)}}$.
This theorem shows that a symmetric body can be always approximated by a 0-regular zonotope as close as we want. Note that the choice of the sequence ${X_{0}^{(N)}}$ is not the best one. Indeed, by taking $\frac{\operatorname{diam}(X)}{\operatorname{diam}({X_{0}^{(N)}})}{X_{0}^{(N)}}$ there is a finer approximation with respect to the Hausdorff distance. However, the sequence ${X_{0}^{(N)}}$ presents some important advantages: it always contains X, the approximation of a Minkowski sum is the Minkowski sum of the approximations, and its face length vector is expressed only from a linear combination of the Feret diameter of X. Furthermore, if there exists $M>1$ such that $X\in {\mathcal{C}_{0}^{(M)}}$, then ${X_{0}^{(M)}}=X$, and X is an adhesion value of the sequence ${X_{0}^{(N)}}$.
Remark 2 (Equivalence between perimeter and maximal diameter).
Notice that $\operatorname{diam}(X)$ can be replaced by $\frac{1}{2}U(X)$ in relation (11). In fact, for any convex set X, we have the relation
Indeed, according to the definition of $\operatorname{diam}(X)$, there exists a line segment $S\subseteq X$ that has the length greater than $\operatorname{diam}(X)$, and then $U(X)\ge U(S)\ge 2\operatorname{diam}(X)$. The second inequality comes by considering that there is a square of side $\operatorname{diam}(X)$ containing X.
Remark 3 (Expression of the mixed area from the Feret diameter).
An interpretation of the mixed area between a convex set and a symmetric convex set can be given from Theorem 3. Indeed, let $N>1$, Y be a convex set (not necessarily symmetric), X be a symmetric convex set, and ${X_{0}^{(N)}}={\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}}$ be its ${\mathcal{C}_{0}^{(M)}}$-approximation. Then, according to the continuity of the area and the Minkowski addition, there is
Furthermore, according to Theorem 3, $W(Y,{X_{0}^{(N)}})$ can be expressed as
\[ W\big(Y,{X_{0}^{(N)}}\big)={\sum \limits_{i=1}^{N}}H_{Y}(\theta _{i}){\sum \limits_{j=1}^{N}}{{F_{ij}^{(N)}}}^{-1}H_{X}(\theta _{j}).\]
Then, the mixed area $W(Y,X)$ can be computed as
Notice that a continuous version of this expression can be written in terms of convolution. However, this is not our objective.Of course, the ${\mathcal{C}_{0}^{(N)}}$-approximation is sensitive to rotations (see Fig. 1). Obviously, it can be problematic to describe the geometry of sets. Let us consider the following example of an ellipse.
Example 1.
Let X be an ellipse with semiaxis $a=1$ and $b=3$, and suppose that the major semiaxis b is horizontally oriented. Firstly, consider the case $N=2$, and let us denote ${X^{\prime }}:=R_{\frac{\pi }{4}}(X)$, Fig. 1 shows that the ${\mathcal{C}_{0}^{(N)}}$-approximation of X is better than that of ${X^{\prime }}$ (in terms of the Hausdorff distance). Indeed, $d_{H}(X,{X_{0}^{(2)}})\ll d_{H}({X^{\prime }},{X^{\prime (2)}_{0}})$. Furthermore, the ${\mathcal{C}_{0}^{(2)}}$-approximation of the rotation is not the rotation of the ${\mathcal{C}_{0}^{(2)}}$-approximation. Therefore, it can be problematic to use the ${\mathcal{C}_{0}^{(2)}}$-approximation to describe the shape of X. Note that for the ellipse X of Fig. 1, the orientations 0 and $\frac{\pi }{4}$ are respectively the better and the worst cases for the ${\mathcal{C}_{0}^{(2)}}$-approximation.
Let us consider now the more general case of the approximation of the rotations of X for different values of N. For each $N=1,\dots ,20$, the ${\mathcal{C}_{0}^{(N)}}$-approximations of all of the rotations $R_{\eta }(X)$ of X have been computed. Among these approximations, the better $\eta _{b}$ and the worst $\eta _{w}$ angles (in terms of the Hausdorff distance) have been retain. The corresponding Hausdorff distances are represented in Fig. 2. Consequently, whatever the orientation of the ellipse, the Hausdorff distance is inside the gray region. We can be notice that, for small values of N, the difference between the worst and the better case is more important.
2.3 Approximation of a symmetric convex set by a regular zonotope
We have shown previously how a symmetric convex set X can be approximated in the class of 0-regular zonotopes. Such an approximation is sensitive to the rotations. However, in order to study convex sets, there is sometimes a need to have isometric invariant tools. Therefore, we will define here an approximation that is invariant up to a rotation. To meet this goal, there is a need to perform the approximation on a class larger than ${\mathcal{C}_{0}^{(N)}}$, namely the class of regular zonotopes.
Definition 4 (t-regular and regular zonotopes).
Let $t\in \mathbb{R}$, $N>1$ be an integer, and let ${\mathcal{C}_{t}^{(N)}}$ denote the class of the rotated elements of ${\mathcal{C}_{0}^{(N)}}$ with respect to the angle t:
Any element of ${\mathcal{C}_{t}^{(N)}}$ is called a t-regular zonotope with $2N$ faces.
Furthermore, ${\mathcal{C}_{\infty }^{(N)}}=\bigcup _{t\in \mathbb{R}}{\mathcal{C}_{t}^{(N)}}$ denotes the set of regular zonotopes with $2N$ faces.
All the properties of ${\mathcal{C}_{0}^{(N)}}$ cited before are also true for ${\mathcal{C}_{t}^{(N)}}$, $t\in \mathbb{R}$. Therefore, we will define an approximation in ${\mathcal{C}_{\infty }^{(N)}}$.
Theorem 2 (Approximation in ${\mathcal{C}_{\infty }^{(N)}}$).
Let $X\in \mathcal{C}$, and let us denote by ${X_{0}^{N}}(t)$ the ${\mathcal{C}_{0}^{(N)}}$-approximation of $R_{-t}(X)$.
The set $R_{\tau }({X_{0}^{N}}(\tau ))$ is called a ${\mathcal{C}_{\infty }^{N}}$-approximation of X in ${\mathcal{C}_{\infty }^{(N)}}$ and is denoted by ${X_{\infty }^{(N)}}$.
-
1. There exists $\tau \in [0,\pi [$ satisfyingWe call ${X_{0}^{N}}(\tau )$ (also denoted ${\tilde{X}_{0}^{N}}$) the ${\mathcal{C}_{0}^{(N)}}$-rotational approximation of X.
(17)
\[ d_{H}\big(R_{\tau }\big({X_{0}^{N}}(\tau )\big),X\big)=d_{H}\big({X_{0}^{N}}(\tau ),R_{-\tau }(X)\big)=\underset{t\in \mathbb{R}}{\min }d_{H}\big({X_{0}^{N}}(t),R_{-t}(X)\big).\] -
2. The ${\mathcal{C}_{0}^{(N)}}$-rotational approximation of X is invariant under rotations of X.
Proof.
$\hspace{0.2222em}$
□
-
1. First of all, because of the symmetry of the 0-regular zonotopes,\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \forall t\in \mathbb{R},\hspace{1em}{\mathcal{C}_{t}^{(N)}}={\mathcal{C}_{t+\pi }^{(N)}}\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle \underset{t\in \mathbb{R}}{\min }d_{H}\big({X_{0}^{N}}(t),R_{-t}(X)\big)=\underset{t\in [0,\pi ]}{\min }d_{H}\big({X_{0}^{N}}(t),R_{-t}(X)\big).\end{array}\]For any $t\in \mathbb{R}$, let us denote by $\alpha (t)$ the face length vector of ${X_{0}^{N}}(t)$. Then, for any $h\in \mathbb{R}$,\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \big\| \alpha (t)-\alpha (t+h)\big\| _{_{1}}=\big\| {{F}^{(N)}}^{-1}\big({H_{R_{-t}(X)}^{(N)}}-{H_{R_{-t-h}(X)}^{(N)}}\big)\big\| _{_{1}}\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle \big\| \alpha (t)-\alpha (t+h)\big\| _{_{1}}\le \big\| {{F}^{(N)}}^{-1}\big\| _{_{1}}\big\| {H_{R_{-t}(X)}^{(N)}}-{H_{R_{-t-h}(X)}^{(N)}}\big\| _{_{1}}.\end{array}\]However, $\forall \eta \in \mathbb{R}$, $H_{R_{-t-h}(X)}(\eta )=H_{R_{-t}(X)}(\eta +h)$. Because of the continuity of the Feret diameter, $\| {H_{R_{-t}(X)}^{(N)}}-{H_{R_{-t-h}(X)}^{(N)}}\| _{_{1}}\to 0$ as $h\to 0$, and thus $\| \alpha (t)-\alpha (t+h)\| _{_{1}}\to 0$ as $\to 0$.Therefore, from expression (7) about the Feret diameter of a zonotope, for all $\eta \in \mathbb{R}$,\[\begin{array}{r@{\hskip0pt}l}\displaystyle \big|H_{{X_{0}^{N}}(t+h)}(\eta )-H_{{X_{0}^{N}}(t)}(\eta )\big|& \displaystyle =\bigg|\Bigg({\sum \limits_{i=1}^{N}}\big(\alpha _{i}(t)-\alpha _{i}(t+h)\big)\big|\sin (\eta -\theta _{i})\big|\Bigg)\bigg|\\{} & \displaystyle \le N\underset{i=1,\dots ,N}{\max }\big\{\big(\alpha _{i}(t)-\alpha _{i}(t+h)\big)\big\}.\end{array}\]Therefore, $|H_{{X_{0}^{N}}(t+h)}(\eta )-H_{{X_{0}^{N}}(t)}(\eta )|\to 0$ as $h\to 0$, and, finally, $d_{H}({X_{0}^{N}}(t),{X_{0}^{N}}(t+h))\to 0$ as $h\to 0$. Consequently, the map $t\mapsto {X_{0}^{N}}(t)$ is continuous with respect to the Hausdorff distance.Note that for all $x\in \mathbb{R}$, $H_{R_{t}({X_{0}^{N}}(t))}(x)=H_{{X_{0}^{N}}(t)}(x-t)$ and $H_{X}(x)=H_{R_{-t}(X)}(x-t)$. Then\[\begin{array}{r@{\hskip0pt}l}& \displaystyle H_{R_{t}({X_{0}^{N}}(t))}(x)-H_{X}(x)=H_{{X_{0}^{N}}(t)}(x-t)-H_{R_{-t}(X)}(x-t)\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle d_{H}\big(R_{t}\big({X_{0}^{N}}(t)\big),X\big)=d_{H}\big({X_{0}^{N}}(t),R_{-t}(X)\big)\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle \underset{t\in \mathbb{R}}{\min }d_{H}\big(R_{t}\big({X_{0}^{N}}(t)\big),X\big)=\underset{t\in \mathbb{R}}{\min }d_{H}\big({X_{0}^{N}}(t),R_{-t}(X)\big).\end{array}\]Furthermore, for any $x,h\in \mathbb{R}$,\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \big|H_{R_{t}({X_{0}^{N}}(t))}(x)-H_{R_{t+h}({X_{0}^{N}}(t+h))}(x)\big|\\{} & \displaystyle \hspace{1em}=\big|H_{{X_{0}^{N}}(t)}(x-t)\\{} & \displaystyle \hspace{2em}-\cdots -H_{{X_{0}^{N}}(t+h)}(x-t)+H_{{X_{0}^{N}}(t+h)}(x-t)-H_{{X_{0}^{N}}(t+h)}(x-t-h)\big|\\{} & \displaystyle \hspace{1em}\le \big|H_{{X_{0}^{N}}(t)}(x-t)-H_{{X_{0}^{N}}(t+h)}(x-t)\big|\\{} & \displaystyle \hspace{2em}+\cdots +\big|H_{{X_{0}^{N}}(t+h)}(x-t)-H_{{X_{0}^{N}}(t+h)}(x-t-h)\big|.\end{array}\]Then from the continuity of the Feret diameter and of the map $t\mapsto X_{N}(t)$ there follows the continuity of $t\mapsto R_{t}({X_{0}^{N}}(t))$. As a consequence, the map $t\mapsto d_{H}({X_{0}^{N}}(t),X)$ is also continuous, and the minimum $\min _{t\in [0,\pi ]}d_{H}(R_{t}({X_{0}^{N}}(t)),X)$ is achieved. Then there is $a\in [0,\pi ]$ such that $d_{H}(R_{\tau }({X_{0}^{N}}(\tau )),X)=\min _{t\in \mathbb{R}}d_{H}({X_{0}^{N}}(t),R_{-t}(X))$.
-
2. Let us prove the invariance by rotations. Let $\eta \in [0,\pi ]$ and $Y=R_{\eta }(X)$. Then ${Y_{0}^{N}}(t)$ is the ${\mathcal{C}_{0}^{(N)}}$-approximation of $R_{-(t-\eta )}(X)$, and ${Y_{0}^{N}}(t)={X_{0}^{N}}(t-\eta )$. Furthermore,\[\begin{array}{r@{\hskip0pt}l}\displaystyle \underset{t\in \mathbb{R}}{\min }d_{H}\big({Y_{0}^{N}}(t),R_{-t}(Y)\big)& \displaystyle =\underset{t\in \mathbb{R}}{\min }d_{H}\big({X_{0}^{N}}(t-\eta ),R_{-(t-\eta )}(X)\big)\\{} & \displaystyle =\underset{t\in \mathbb{R}}{\min }d_{H}\big({X_{0}^{N}}(t),R_{-(t)}(X)\big)\\{} & \displaystyle =d_{H}\big({X_{0}^{N}}(\tau ),R_{-\tau }(X)\big).\end{array}\]Then ${X_{0}^{N}}(\tau )$ is a ${\mathcal{C}_{0}^{(N)}}$-rotational approximation of Y, and the ${\mathcal{C}_{\infty }^{(N)}}$-approximation associated is $R_{\eta }(R_{\tau }({X_{0}^{N}}(\tau )))$ (indeed, ${Y_{0}^{N}}(\tau +\eta )={X_{0}^{N}}(\tau )$).
The theorem gives important information. The ${\mathcal{C}_{\infty }^{(N)}}$-approximation of a symmetric convex set X is the best regular zonotope with at most $2N$ faces containing X. It is always a better approximation than the ${\mathcal{C}_{0}^{(N)}}$-approximation. This approximation can be used for not so large N. For example, for $N=2$, the ${\mathcal{C}_{0}^{(2)}}$-approximation of an ellipse depends on the orientation of the ellipse, but its ${\mathcal{C}_{\infty }^{(2)}}$-approximation is the best way to put the ellipse inside a rectangle (see Fig. 3). An illustration of the approximations of that ellipse for higher values of N is represented Fig. 4.
Fig. 3.
An ellipse and its approximations: $X_{2}\in {\mathcal{C}_{0}^{(2)}}$ in blue and $R_{\tau }(\tilde{X}_{2})\in {\mathcal{C}_{\infty }^{(2)}}$ in red
Fig. 4.
The ${\mathcal{C}_{0}^{(N)}}$-approximations (left) and ${\mathcal{C}_{\infty }^{(N)}}$-approximations (right) of an ellipse of semiaxis $(3,1)$ for different values of $N(=3,4,10)$
The accuracy of the ${\mathcal{C}_{0}^{(N)}}$-approximation is presented in Fig. 2, and we remark that the best orientation corresponds to the ${\mathcal{C}_{\infty }^{(N)}}$-approximation. Then, for the considered ellipse, the accuracy of the ${\mathcal{C}_{\infty }^{(N)}}$-approximation in function of the number of faces N is represented in Fig. 2. However, the accuracy of the ${\mathcal{C}_{\infty }^{(N)}}$-approximation depends on both shape and size of the symmetric convex set X.
Fig. 5.
The Hausdorff distance between an ellipse of unit perimeter and its ${\mathcal{C}_{\infty }^{(N)}}$-approximations for several values of N in function of its axis ratio k
Remark 4 (Accuracy of the ${\mathcal{C}_{\infty }^{(N)}}$-approximation).
The size dependence of the accuracy is easy to understand: the accuracy decreases proportionally to the size factor. Indeed, for $Y:=kX$, $k\in \mathbb{R}_{+}$, we have $d_{H}({Y_{\infty }^{(N)}},Y)=kd_{H}({X_{\infty }^{(N)}},X)$ (because of the homogeneity of the Feret diameter). In order to study the impact of the shape (independently of its size) on the approximation accuracy, we need to use a homothetic invariant descriptor. In order to do this, we normalize the Feret diameter of a symmetric convex set X by its perimeter. According to Cauchy’s formula [27], the perimeter is equal to the Feret diameter total mass ${\int _{0}^{\pi }}H_{X}(\theta )d\theta $. Then, according to the homogeneity of the Feret diameter, an involved distance can be defined as $\tilde{d}_{H}(X,Y):=d_{H}(\frac{X}{U(X)},\frac{Y}{U(Y)})$ for all $X,Y\in \mathcal{C}$. Such a distance can be used to study the approximation accuracy. Notice that it is equivalent to work with sets of unit perimeters and using the usual Hausdorff distance. Such a consideration will be done in the following example.
Let us consider an ellipse X with unit perimeter and axis ratio $k\in [1,+\infty [$, the case $k=1$ referring to the disk. The accuracy of the ${\mathcal{C}_{\infty }^{(N)}}$-approximation as a function of N and k is shown. More specifically, on the Fig. 5, we can see that the behavior of the curves is very different for different values of N. Indeed, the worst shape for $N=2$ is the disk. However, as we can see that this is not the case for other values of N. We can notice that when the ratio k increases, the importance of N for the approximation decreases. This suggests that when an object X is elongated, we can choose a small value of N.
We have studied two different approximations of a symmetric convex set X. The first one is an approximation of X as a 0-regular zonotope, and the second as a regular zonotope. These approximations have been characterized from the Feret diameter of X. The next objective is to study these approximations when X becomes a random symmetric body, and then how they can be characterized from the Feret diameter of X. In order to do this, we need to study some properties of the random zonotopes, which lead us to the following section.
3 The random zonotopes
The aim of this section is to investigate how a random zonotope can be described by a random vector representing its faces and how such a random vector can be characterized from the Feret diameter of the random zonotope. Firstly, we will investigate the properties of the random process corresponding to the Feret diameter of a random set. Secondly, we will explore the description of a random zonotope by its faces. Finally, we will give a characterization of some random zonotopes from their Feret diameter random process.
3.1 Feret diameter process and isotropic random set
Let X be a random convex set, that is, a random closed set that is almost surely a convex set. In this subsection, we state some properties of the random process [9] corresponding to the Feret diameter of X.
Definition 5 (Feret diameter random process).
Let X be a random convex set of ${\mathbb{R}}^{2}$. For P-almost all $\omega \in \varOmega $, $X(\omega )$ is a convex set. Then, for any $t\in \mathbb{R}$, the positive random variable $H_{X}(t):\omega \mapsto H_{X(\omega )}(t)$ is almost surely defined. The random process $\{H_{X}(t),t\in \mathbb{R}\}$ is called the Feret diameter random process of X.
The trajectories of $H_{X}$ are the Feret diameter of the realizations of X. The properties in Proposition 2 are also true for these trajectories, in particular, the continuity and π-periodicity. We can also notice that the Feret diameter random process characterizes the symmetric convex sets.
Definition 6 (Isotropized set of a random symmetric body).
Let ${X^{\prime }}$ be a symmetric random convex set, and let η be a random uniform variable on $[0,\pi ]$ independent of ${X^{\prime }}$. Then the set
is isotropic (a random compact is said to be isotropic if and only if its distribution is isometric invariant [8]) and is called an isotropized set of ${X^{\prime }}$.
Let ${X^{\prime }}$ be a random symmetric body, and X be an isotropized set of it. Then X and ${X^{\prime }}$ have the same shape distribution and the same zonotope rotational approximations (see Theorem 2).
In the following, we will show that the Feret diameter random process $H_{{X^{\prime }}}$ of ${X^{\prime }}$ can be expressed from that of X. We will use this property to show that a random symmetric convex set can be described up to a rotation by an isotropic random zonotope.
Let us recall that the Feret diameter random process $H_{{X^{\prime }}}$ of ${X^{\prime }}$ is sufficient to characterize ${X^{\prime }}$. Then, for any $\theta \in \mathbb{R}$, the Feret diameter $H_{{X^{\prime }}}$ of ${X^{\prime }}$ can be expressed as
Let B be a Borel subset of $\mathbb{R}$. Because of the uniformity of η and its independence from ${X^{\prime }}$, it follows that
Consequently, the moments of the Feret diameter process of the set ${X^{\prime }}$ and the isotropized set X are related. Of course, we need to ensure their existence, but we will treat this later.
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathbb{P}\big(H_{X}(\theta )\in B\big)& \displaystyle =\mathbb{P}\big(H_{{X^{\prime }}}(\theta -\eta )\in B\big)\\{} & \displaystyle =\frac{1}{2\pi }{\int _{0}^{2\pi }}\mathbb{P}\big(H_{{X^{\prime }}}(\theta -t)\in B\big)\hspace{0.1667em}dt.\end{array}\]
Furthermore, by using the π-periodicity of the Feret diameter the distribution of $H_{X}(\theta )$ can be expressed as
(18)
\[ \mathbb{P}\big(H_{X}(\theta )\in B\big)=\frac{1}{\pi }{\int _{0}^{\pi }}\mathbb{P}\big(H_{{X^{\prime }}}(\theta -t)\in B\big)\hspace{0.1667em}dt.\]Proposition 4 (Moments of the Feret diameter process of the isotropized set).
Let ${X^{\prime }}$ be a random convex set, and X the isotropized set of ${X^{\prime }}$. Suppose that the first- and second-order moments of the Feret diameter random process $H_{{X^{\prime }}}$ of ${X^{\prime }}$ exist.Then those of X exist and can be expressed as follows:
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \forall \theta \in [0,2\pi ],\hspace{1em}\mathbb{E}\big[H_{X}(\theta )\big]=\frac{1}{\pi }{\int _{0}^{\pi }}\mathbb{E}\big[H_{{X^{\prime }}}(\theta )\big]\hspace{0.1667em}d\theta ,\\{} & \displaystyle \forall (s,t)\in {[0,2\pi ]}^{2},\hspace{1em}\mathbb{E}\big[H_{X}(s)H_{X}(t)\big]=\frac{1}{\pi }{\int _{0}^{\pi }}\mathbb{E}\big[H_{{X^{\prime }}}(\theta )H_{{X^{\prime }}}(\theta +s-t)\big]\hspace{0.1667em}d\theta .\end{array}\]
Proof.
Let ${X^{\prime }}$ be a random convex set, and $X=R_{\eta }({X^{\prime }})$ an isotropized set of it. Suppose that the first- and second-order moments of $H_{{X^{\prime }}}$ exist. Recall that $H_{X}(\theta )=H_{{X^{\prime }}}(\theta -\eta )$ for all $\theta \in \mathbb{R}$ and that η is independent of ${X^{\prime }}$, and thus the result follows by integrating with respect to the uniform distribution of η. □
Proposition 5 (Feret diameter process of an isotropic random convex set).
Let ${X^{\prime }}$ be a random convex set.
Proof.
-
1. Let η be a uniform random variable on $[0,\pi ]$ independent of ${X^{\prime }}$ and let note $X=R_{\eta }({X^{\prime }})$. If ${X^{\prime }}$ is isotropic, then X and ${X^{\prime }}$ have the same distribution, so that $H_{X}$ and $H_{{X^{\prime }}}$ also have the same distribution. Consequently, according to (18), for any $\theta \in [0,\pi ]$ and any Borel set B,\[ \mathbb{P}\big(H_{{X^{\prime }}}(\theta )\in B\big)=\mathbb{P}\big(H_{X}(\theta )\in B\big)=\frac{1}{\pi }{\int _{0}^{\pi }}\mathbb{P}\big(H_{{X^{\prime }}}(\theta -t)\in B\big)\hspace{0.1667em}dt.\]Because of the π-periodicity of the Feret diameter, the integral is independent of θ, and thus the random variables $H_{{X^{\prime }}}(\theta )$, $\theta \in [0,\pi ]$, are identically distributed.
-
2. Suppose that ${X^{\prime }}$ is symmetric and $H_{{X^{\prime }}}(\theta )$, $\theta \in [0,\pi ]$, are identically distributed. Then the random process $H_{{X^{\prime }}}$ is stationary, that is, for any $x\in \mathbb{R}$, the random process $(H_{{X^{\prime }}}(\theta ))_{\theta \in \mathbb{R}}$ and the translated process $(\tilde{H}_{{X^{\prime }}}(\theta )=H_{{X^{\prime }}}(\theta +x))_{\theta \in \mathbb{R}}$ have the same distribution. However, $\tilde{H}_{{X^{\prime }}}$ is exactly the random process corresponding to the Feret diameter of $R_{x}({X^{\prime }})$. It has been already established that the Feret diameter characterizes the symmetric bodies. Therefore, for any $x\in \mathbb{R}$, $R_{x}({X^{\prime }})$ and ${X^{\prime }}$ have the same distribution, so that ${X^{\prime }}$ is isotropic.
We have shown some properties of the Feret diameter random process. Let us discuss now the random zonotopes, that is, the random sets almost surely valued in ${\mathcal{C}}^{(N)}$.
3.2 Description of the random zonotopes from their faces
Here we will define some classes of random zonotopes, in particular, the class of the random zonotopes almost surely valued in ${\mathcal{C}_{0}^{(N)}}$ and the class of those almost surely valued in ${\mathcal{C}_{\infty }^{(N)}}$. We will study several properties of the random zonotopes. In particular, we will show how a random zonotope can be described by a random vector corresponding to its faces.
Definition 7 (Random zonotopes).
For an integer $N>1$, a random closed set X that has realizations almost surely in ${\mathcal{C}}^{(N)}$ is called a random zonotope with at most $2N$ faces or, in a more concise way, a random zonotope when there is no possible confusion.
Such a random set can be described almost surely as
\[ \forall \omega \in \varOmega \hspace{2.5pt}\text{a.s.},\hspace{1em}X(\omega )={\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}(\omega )S_{\beta _{i}(\omega )}.\]
The distribution of the random vector $(\alpha ,\beta )$ characterizes X. The random vector α is called a face length vector of X.According to Proposition 3, for any face length vector α of X, some geometrical characteristics (Feret diameter, perimeter, area) of X can be expressed as:
(19)
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \forall \omega \in \varOmega \hspace{2.5pt}\text{a.s.},\hspace{2.5pt}\forall t\in \mathbb{R},\hspace{1em}H_{X}(t)& \displaystyle ={\sum \limits_{i=1}^{N}}\alpha _{i}\big|\sin (t-\beta _{i})\big|;\end{array}\]Proposition 6 (Existence conditions for the autocovariance of the Feret diameter process).
Let X be a random zonotope with $2N$ faces, and α its face length vector. Then the following properties are equivalent:
Furthermore, if one of these conditions is satisfied, then $\mathbb{E}[A(X)]<\infty $, and $\mathbb{E}[H_{X}(s)H_{X}(t)]<\infty $ for all $(s,t)\in {[0,\pi ]}^{2}$.
Proof.
According to (20), $U{(X)}^{2}={(2{\sum _{i=1}^{N}}\alpha _{i})}^{2}$, and the first equivalence is trivial (because of the positivity of α).
Proposition 3 also shows that, for all $(s,t)\in {[0,\pi ]}^{2}$,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle H_{X}(s)H_{X}\big({t^{\prime }}\big)& \displaystyle ={\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}\alpha _{i}\alpha _{j}\big|\sin (s-\eta -\beta _{i})\sin (t-\eta -\beta _{i})\big|\\{} & \displaystyle \le {\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}\alpha _{i}\alpha _{j}\\{} & \displaystyle \le \frac{1}{4}U{(X)}^{2}.\end{array}\]
Then the expectation $\mathbb{E}[H_{X}(s)H_{X}(t)]$ exists, and the existence of $\mathbb{E}[A(X)]$ follows from the isoperimetric inequality. □Definition 8 (0-regular random zonotopes).
For an integer $N>1$, a random closed set X that has its realizations almost surely in ${\mathcal{C}_{0}^{(N)}}$ is called a 0-regular random zonotope with at most $2N$ faces or, in a more concise way, a 0-regular random zonotope when there is no possible confusion.
A 0-regular random zonotope X can be almost surely expressed as
\[ \forall \omega \in \varOmega \hspace{2.5pt}\text{a.s.},\hspace{1em}X(\omega )={\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}(\omega )S_{\theta _{i}},\]
where $\theta _{i}$, $i=1,\dots ,N$, denotes the regular subdivision on $[0,\pi ]$.The distribution of the face length vector α characterizes the distribution of X. In addition, this relation is bijective; in other word, the distribution of α is uniquely defined and is called the face length distribution.
Of course, the 0-regular random zonotopes can be used to approximate the random symmetric convex sets as $N\to \infty $ (see Section 4.1). However, it is not the best way to model a random symmetric convex set. Indeed, notice that a 0-regular random zonotope cannot be isotropic. For instance, we need to use a large N in order to describe a random set built as an isotropic random square; see Example 3. This is the reason for using a larger class of random zonotopes.
Definition 9 (Regular random zonotopes).
For an integer $N>1$, any random compact set taking its values almost surely in ${\mathcal{C}_{\infty }^{(N)}}$ is called a regular random zonotope and can be expressed as
where x is a random variable on $[0,\pi ]$, and α is a random vector taking values in ${\mathbb{R}_{+}^{N}}$. The random vector α is called a random face length vector of X.
Proposition 7 (Isotropic regular random zonotope).
Let $X=R_{x}({\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}})$ be an isotropic regular random zonotope. Then X has the same distribution of the following random set:
where η is a uniform random variable on $[0,\pi ]$ independent of α.
(24)
\[ X\stackrel{a.s.}{=}R_{\eta }\Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}S_{\theta _{i}}\Bigg),\]Proof.
Let $X=R_{x}({\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}})$ be an isotropic regular random zonotope, and ${\eta ^{\prime }}$ be a uniform random variable independent of α. Because of the isotropy of X, the random set $R_{{\eta ^{\prime }}}(X)$ has the same distribution as X. Let $\eta =x+{\eta ^{\prime }}[\pi ]$. Then the random set $R_{{\eta ^{\prime }}}(X)$ can be expressed as $R_{\eta }({\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}})$. Consequently, $R_{\eta }({\bigoplus _{i=1}^{N}}\alpha _{i}S_{\theta _{i}})$ has the same distribution as X.
Let us show that η is a uniform variable independent of α.
Let B be a Borel set of ${\mathbb{R}}^{N}$, and let $E=\{\eta \in [0,t]\}\cap \{\alpha \in B\}$ for any $t\in [0,\pi ]$. Then
\[\begin{array}{r@{\hskip0pt}l}\displaystyle E& \displaystyle =\{\alpha \in B\}\cap \bigg(\bigcup \limits_{z\in [0,\pi ]}\{x=z\}\cap \big\{{\eta ^{\prime }}+z[\pi ]\le t\big\}\bigg)\\{} & \displaystyle =\bigcup \limits_{z\in [0,\pi ]}\{\alpha \in B\}\{x=z\}\cap \big\{{\eta ^{\prime }}+z[\pi ]\le t\big\}.\end{array}\]
Note that this union is disjointed. Then because of the independence of ${\eta ^{\prime }}$,
\[ \mathbb{P}(E)={\int _{0}^{\pi }}\mathbb{P}\big(\{\alpha \in B\}\{x=z\}\big)\mathbb{P}\big(\big\{{\eta ^{\prime }}+z[\pi ]\le t\big\}\big)\hspace{0.1667em}dz.\]
The quantity $\mathbb{P}(\{{\eta ^{\prime }}+z[\pi ]\le t\})$ is independent of the value of z and can be easily computed as $\mathbb{P}(\{{\eta ^{\prime }}+z[\pi ]\le t\})=\frac{t}{\pi }$. Consequently:
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathbb{P}(E)& \displaystyle =\frac{t}{\pi }{\int _{0}^{\pi }}\mathbb{P}\big(\{\alpha \in B\}\{x=z\}\big)\mathbb{P}\big(\big\{{\eta ^{\prime }}+z[\pi ]\le t\big\}\big)\hspace{0.1667em}dz,\\{} \displaystyle \mathbb{P}(E)& \displaystyle =\frac{t}{\pi }\mathbb{P}\big(\{\alpha \in B\}\big).\end{array}\]
Then η is a uniform random variable on $[0,\pi ]$ independent of α. □This proposition shows that an isotropic regular random zonotope can always be described as in (24). Such a zonotope is consequently defined by its random face length vector α. However, different distributions of α can lead to the same distribution of X, as mentioned in the following proposition.
Proposition 8 (Family of the random face length vectors).
Let α be a random face length vector of the isotropic regular random zonotope X. The following family of random face length vectors, denoted $\mathcal{F}_{N}(X)$, provides the same distribution of the random set X:
where J is the circulant matrix $J=Circ(0,1,0,\dots ,0)$.
(25)
\[ \mathcal{F}_{N}(X)=\big\{{\alpha ^{\prime }}\stackrel{a.s}{=}{J}^{n}\alpha \big|\forall \omega \in \varOmega \textit{a.s.},n(\omega )\in \{0,\dots ,N-1\}\big\},\]Proof.
First of all, it is easy to see that $\mathcal{F}_{N}(X)$ is not empty by construction of X. Let $\alpha ,{\alpha ^{\prime }}$ be two representative random vectors of X. Then there exist two uniform random variables η and ${\eta ^{\prime }}$ satisfying 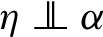 and
and 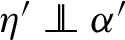 such that:
such that:
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \forall \omega \in \varOmega \hspace{2.5pt}\text{a.s.},\hspace{1em}{\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}(\omega )S_{\theta _{i}+\eta (\omega )}={\underset{i=1}{\overset{M}{\bigoplus }}}{\alpha ^{\prime }_{i}}(\omega )S_{\theta _{i}+{\eta ^{\prime }}(\omega )}\\{} \displaystyle \Rightarrow & \displaystyle \hspace{1em}\forall \omega \in \varOmega \hspace{2.5pt}\text{a.s.},\hspace{1em}R_{-{\eta ^{\prime }}(\omega )}\Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}(\omega )S_{\theta _{i}+\eta (\omega )}\Bigg)=R_{-{\eta ^{\prime }}(\omega )}\Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}{\alpha ^{\prime }_{i}}(\omega )S_{\theta _{i}+{\eta ^{\prime }}(\omega )}\Bigg)\\{} \displaystyle \Rightarrow & \displaystyle \hspace{1em}\forall \omega \in \varOmega \hspace{2.5pt}\text{a.s.},\hspace{1em}{\underset{i=1}{\overset{N}{\bigoplus }}}{\alpha ^{\prime }_{i}}(\omega )S_{\theta _{i}}={\underset{i=1}{\overset{N}{\bigoplus }}}\alpha _{i}(\omega )S_{\theta _{i}+\eta (\omega )-{\eta ^{\prime }}(\omega )}.\end{array}\]
Then, because of the uniqueness of the face length vector in ${\mathcal{C}_{0}^{(N)}}$, for any $\omega \in \varOmega $ a.s., there is $j(\omega )\in \{1,\dots ,N\}$ such that
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \theta _{1}=\big(\theta _{j(\omega )}+\eta (\omega )-{\eta ^{\prime }}(\omega )\big)[\pi ]\hspace{2.5pt}\text{and}\hspace{2.5pt}{\alpha ^{\prime }_{1}}(\omega )=\alpha _{j}(\omega )\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle \theta _{j(\omega )}=\big({\eta ^{\prime }}(\omega )-\eta (\omega )\big)[\pi ]\hspace{2.5pt}\text{and}\hspace{2.5pt}{\alpha ^{\prime }_{1}}(\omega )=\alpha _{j}(\omega )\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle {\alpha ^{\prime }_{i}}(\omega )=\alpha _{i+j-1[M]}(\omega )\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle {\alpha ^{\prime }}(\omega )={J}^{j(\omega )-1}\alpha (\omega ).\end{array}\]
By taking $\forall \omega \in \varOmega $ a.s., $n(\omega )=j(\omega )-1[N]$ it follows that ${\alpha ^{\prime }}={J}^{n}\alpha $ and, consequently, $\mathcal{F}_{N}(X)\subset \{{\alpha ^{\prime }}={J}^{n}\alpha |\forall \omega \in \varOmega $ a.s., $n(\omega )\in \{0,\dots ,N-1\}\}$.The other inclusion can be proved by taking ${\eta ^{\prime }}$ such that $\forall \omega \in \varOmega $ a.s., ${\eta ^{\prime }}(\omega )=\beta _{n(\omega )+1}+\eta [\pi ]$. For such ${\eta ^{\prime }}$, it follows that $\forall \omega \in \varOmega $ a.s., $X(\omega )={\bigoplus _{i=1}^{N}}{\alpha ^{\prime }_{i}}(\omega )S_{\theta _{i}+{\eta ^{\prime }}(\omega )}$. □
Definition 10 (Central random face length vector).
Let $\alpha \in \mathcal{F}_{N}(X)$, and let n be a uniform random variable on $\{0,\dots ,M-1\}$ independent of α. Then the random face length vector ${\alpha ^{\prime }}={J}^{n}\alpha $ is called a central random face length vector of X.
Notice that a central random face length vector has all components identically distributed. Furthermore, its distribution has many interesting properties.
Proposition 9 (Uniqueness of the central face length distribution).
There is a unique distribution for any central random face length vectors. In other words, let ${\tilde{\alpha }^{\prime }},{\alpha ^{\prime }}$ be two central random face length vectors of X. Then they have same distribution. Such a distribution will be named the central face length distribution of X.
Proof.
Let ${\tilde{\alpha }^{\prime }}$ and ${\alpha ^{\prime }}$ be two central representations of X. Then there exist a random face length vector $\tilde{\alpha }$ and an independent uniform variable $\tilde{n}$ on $\{0,\dots ,N-1\}$ such that ${\tilde{\alpha }^{\prime }}={J}^{\tilde{n}}\tilde{\alpha }$. In addition, $\tilde{\alpha }\in \mathcal{F}_{N}(X)$, so there exists n such that $\tilde{\alpha }={J}^{n}{\alpha ^{\prime }}$. Consequently, ${\tilde{\alpha }^{\prime }}={J}^{\tilde{n}+n}{\alpha ^{\prime }}$. Let ${n^{\prime }}=\tilde{n}+n[N]$. It is easy to see that ${J}^{\tilde{n}+n}={J}^{{n^{\prime }}}$, and thus
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle {\tilde{\alpha }^{\prime }}={J}^{{n^{\prime }}}{\alpha ^{\prime }}.\end{array}\]
Let us prove that ${n^{\prime }}$ is a uniform variable on $\{0,\dots ,M-1\}$ independent of ${\alpha ^{\prime }}$.For any $k\in \{0,\dots ,N-1\}$,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathbb{P}\big(\big\{{n^{\prime }}=k\big\}\big)& \displaystyle =\mathbb{P}\Bigg({\bigcup \limits_{i=0}^{N-1}}\big\{\tilde{n}=k-i[N]\big\}\cap \{n=i\}\Bigg)\\{} & \displaystyle ={\sum \limits_{i=0}^{N-1}}\mathbb{P}\big(\big\{\tilde{n}=k-i[N]\big\}\big)\mathbb{P}\big(\{n=i\}\big)\\{} & \displaystyle =\frac{1}{N}.\end{array}\]
Then ${n^{\prime }}$ is a uniform variable on $\{0,\dots ,N-1\}$. Furthermore, for any Borel set B and any $k\in \{0,\dots ,N-1\}$,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathbb{P}\big(\big\{{n^{\prime }}=k\big\}\cap \big\{{\alpha ^{\prime }}\in B\big\}\big)& \displaystyle =\mathbb{P}\Bigg({\bigcup \limits_{i=0}^{N-1}}\big\{\tilde{n}=k-i[N]\big\}\cap \{n=i\}\cap \big\{{\alpha ^{\prime }}\in B\big\}\Bigg)\\{} & \displaystyle ={\sum \limits_{i=0}^{N-1}}\mathbb{P}\big(\big\{\tilde{n}=k-i[N]\big\}\cap \{n=i\}\cap \big\{{\alpha ^{\prime }}\in B\big\}\big)\\{} & \displaystyle ={\sum \limits_{i=0}^{N-1}}\mathbb{P}\big(\big\{\tilde{n}=k-i[N]\big\}\big)\mathbb{P}\big(\{n=i\}\cap \big\{{\alpha ^{\prime }}\in B\big\}\big)\\{} & \displaystyle =\frac{1}{N}{\sum \limits_{i=0}^{N-1}}\mathbb{P}\big(\{n=i\}\cap \big\{{\alpha ^{\prime }}\in B\big\}\big)\\{} & \displaystyle =\frac{1}{N}\mathbb{P}\big(\big\{{\alpha ^{\prime }}\in B\big\}\big)\\{} & \displaystyle =\mathbb{P}\big(\big\{{n^{\prime }}=k\big\}\big)\mathbb{P}\big(\big\{{\alpha ^{\prime }}\in B\big\}\big).\end{array}\]
Now let us prove that ${\alpha ^{\prime }}$ and ${\tilde{\alpha }^{\prime }}$ have the same distribution. Let $B=B_{0}\times \cdots \times B_{N-1}$ be a product of Borel sets of $\mathbb{R}$. Firstly, note that $\mathbb{P}({J}^{k}{\alpha ^{\prime }}\in B)=\mathbb{P}({\alpha ^{\prime }}\in B)$ for all $k\in \{0,\dots ,N-1\}$. Indeed, by definition, ${\alpha ^{\prime }}$ can be written as ${\alpha ^{\prime }}={J}^{n}\alpha $ with α a representative of X and n an independent uniform random variable on $\{0,\dots ,N-1\}$. Therefore,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathbb{P}\big(\big\{{\alpha ^{\prime }}\in B\big\}\big)& \displaystyle =\mathbb{P}\Bigg({\bigcup \limits_{i=0}^{N-1}}\big\{{J}^{i}\alpha \in B\big\}\cap \{n=i\}\Bigg)\\{} & \displaystyle =\frac{1}{N}{\sum \limits_{i=0}^{N-1}}\mathbb{P}\big(\big\{{J}^{i}\alpha \in B\big\}\big)\\{} & \displaystyle =\frac{1}{N}{\sum \limits_{i=0}^{N-1}}\mathbb{P}\big(\{\alpha \in B_{i}\times \cdots B_{0}\cdots B_{N-1-i}\}\big).\end{array}\]
In the same manner,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathbb{P}\big(\big\{{J}^{k}{\alpha ^{\prime }}\in B\big\}\big)& \displaystyle =\frac{1}{N}{\sum \limits_{i=0}^{N-1}}\mathbb{P}\big(\big\{{J}^{i+k}\alpha \in B\big\}\big)\\{} & \displaystyle =\frac{1}{N}{\sum \limits_{i=0}^{N-1}}\mathbb{P}\big(\{\alpha \in B_{i+k}\times \cdots B_{0}\cdots B_{N-1-i-k}\}\big)\\{} & \displaystyle =\frac{1}{N}{\sum \limits_{i=0}^{N-1}}\mathbb{P}\big(\{\alpha \in B_{i}\times \cdots B_{0}\cdots B_{N-1-i}\}\big)\\{} & \displaystyle =\mathbb{P}\big(\big\{{\alpha ^{\prime }}\in B\big\}\big).\end{array}\]
Furthermore,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathbb{P}\big(\big\{\tilde{{\alpha ^{\prime }}}\in B\big\}\big)& \displaystyle =\mathbb{P}\Bigg({\bigcup \limits_{k=0}^{N-1}}\big\{{J}^{k}{\alpha ^{\prime }}\in B\big\}\cap \big\{{n^{\prime }}=k\big\}\Bigg)\\{} & \displaystyle =\frac{1}{N}{\sum \limits_{k=0}^{N-1}}\mathbb{P}\big(\big\{{J}^{k}{\alpha ^{\prime }}\in B\big\}\big)\\{} & \displaystyle =\mathbb{P}\big(\big\{{\alpha ^{\prime }}\in B\big\}\big).\end{array}\]
Finally, ${\tilde{\alpha }^{\prime }}$ and ${\alpha ^{\prime }}$ have the same distribution. □Proposition 10 (Properties of the central face length distribution).
Let α be a central random face length vector of X. Then the first- and second-order moments of its distribution have the following properties:
-
2. Second-order moment:The matrix $C[\alpha ]=(\mathbb{E}[\alpha _{i}\alpha _{j}])_{1\le i,j\le N}$ is a circulant matrix defined by the first column $V[\alpha ]={}^{t}(\mathbb{E}[\alpha _{1}\alpha _{1}],\dots ,\mathbb{E}[\alpha _{1}\alpha _{N}])$: $C[\alpha ]=Circ(V[\alpha ])$. Furthermore, this matrix is symmetric and depends only on $(\lfloor \frac{N}{2}\rfloor +1)$ values, where $\lfloor \frac{N}{2}\rfloor $ denotes the floor of $\frac{N}{2}$. Note that $m=\lfloor \frac{N}{2}\rfloor $ and $v={}^{t}(\mathbb{E}[\alpha _{1}\alpha _{1}],\dots ,\mathbb{E}[\alpha _{1}\alpha _{m+1}])$; therefore, if N is an even integer, then $V={}^{t}(v_{0},\dots ,v_{m-1},v_{m},v_{m-1},\dots ,v_{1})$, and if N is an odd integer, then $V={}^{t}(v_{0},\dots ,v_{m},v_{m},\dots ,v_{1})$.
Proof.
$\hspace{0.2222em}$
□
-
1. The first item is trivial. Indeed, the marginals of α are identically distributed. Therefore, $\mathbb{E}[\alpha _{i}]=\mathbb{E}[\alpha _{j}]$ for all $i,j$, and $U(X)=2{\sum _{i=1}^{N}}\alpha _{i}\Rightarrow \hspace{0.2778em}\mathbb{E}[\alpha _{i}]=\frac{U(X)}{2N}$, $i=1,\dots ,N$.
-
2. It has been shown that if, for any $k\in \{0,\dots ,N-1\}$, the random variables α and ${J}^{k}\alpha $ have same distribution, then they have the same covariance matrix. Therefore, for all $1\le i,j\le N$,\[ \forall k\in \{0,\dots ,N-1\},\hspace{1em}\mathbb{E}[\alpha _{i}\alpha _{j}]=\mathbb{E}[\alpha _{i+k[N]+1}\alpha _{j+k[N]+1}],\]so $\mathbb{E}[\alpha _{i}\alpha _{j}]$ is a circulant matrix that depends only on $i-j[N]$ and, because of its symmetry, and on $j-i[N]$. Let $1\le i\le j\le N$. Then there are two possible cases. First, suppose that $N=2m$ is an even integer. Then, for all $0\le k\le m-1$,\[ \mathbb{E}[\alpha _{1}\alpha _{1+m+k}]=\mathbb{E}[\alpha _{1+m}\alpha _{1+k}]=\mathbb{E}[\alpha _{1+m+N-k}\alpha _{1+N}]=\mathbb{E}[\alpha _{1}\alpha _{1+m-k}].\]Note that\[ V={}^{t}\big(\mathbb{E}[\alpha _{1}\alpha _{1}],\dots ,\mathbb{E}[\alpha _{1}\alpha _{N}]\big)\hspace{2.5pt}\hspace{2.5pt}\text{and}\hspace{2.5pt}\hspace{2.5pt}v={}^{t}\big(\mathbb{E}[\alpha _{1}\alpha _{1}],\dots ,\mathbb{E}[\alpha _{1}\alpha _{m+1}]\big).\]Therefore, there is If N is an odd integer, then $N=2m+1$, and for any $0\le k\le m$,\[ \mathbb{E}[\alpha _{1}\alpha _{1+m+k}]=\mathbb{E}[\alpha _{1+m+1}\alpha _{1+k}]=\mathbb{E}[\alpha _{2+m+N-k}\alpha _{1+N}]=\mathbb{E}[\alpha _{1}\alpha _{2+m-k}],\]then by noting that\[ V[\alpha ]={}^{t}\big(\mathbb{E}[\alpha _{1}\alpha _{1}],\dots ,\mathbb{E}[\alpha _{1}\alpha _{N}]\big)\hspace{2.5pt}\hspace{2.5pt}\text{and}\hspace{2.5pt}\hspace{2.5pt}v={}^{t}\big(\mathbb{E}[\alpha _{1}\alpha _{1}],\dots ,\mathbb{E}[\alpha _{1}\alpha _{m+1}]\big)\]there is $V={}^{t}(v_{0},\dots v_{m},v_{m},\dots v_{1})$. Finally, $C[\alpha ]$ is a symmetric circulant matrix.
Example 2.
In order to illustrate the properties of the face length vector distributions, let us discuss the case $N=2$. Then, $X=R_{\eta }(\alpha _{1}S_{0}\oplus \alpha _{2}S_{\frac{\pi }{2}})$ with η a uniform random variable on $[0,\pi ]$ independent of α.
Therefore, X is an isotropic random rectangle described by its sides $(\alpha _{1},\alpha _{2})$. However, this is not the unique way to describe it. Indeed, even for a deterministic rectangle of sides $(a,b)$, we can also say that its sides are $(b,a)$. This simple fact involves a lot of different distributions for the face length vectors of an isotropic random rectangle.
Let us take consider a simple example: suppose that Y is equiprobably the rectangle of sides $(1,2)$ or the rectangle of sides $(3,4)$. Then, there is at least one of the following four possible descriptions for the realization of sides of Y:
Therefore, there are four corresponding face length distributions $\frac{1}{2}\Delta _{(1,2)}+\frac{1}{2}\Delta _{(3,4)}$, $\frac{1}{2}\Delta _{(2,1)}+\frac{1}{2}\Delta _{(3,4)}$,…, where $\Delta _{(a,b)}$ denotes the Dirac measure in $(a,b)$. However, there are not the only possibilities. Indeed, many other can be built from the previous distributions, such as the distribution $\frac{1}{4}\Delta _{(1,2)}+\frac{1}{4}\Delta _{(2,1)}+\frac{1}{2}\Delta _{(3,4)}$. Notice that the central distribution of Y is $\frac{1}{4}\Delta _{(1,2)}+\frac{1}{4}\Delta _{(2,1)}+\frac{1}{4}\Delta _{(3,4)}+\frac{1}{4}\Delta _{(4,3)}$.
Let us return now to the general case of the isotropic random rectangle X with a face length vector α. According to the foregoing, it is easy to see that any another face length vector ${\alpha ^{\prime }}$ of X can be built as
where δ is any Bernoulli variable (i.e., valued in $\{0,1\})$ eventually correlated to α.
(27)
\[ {\alpha ^{\prime }}=\left(\begin{array}{c@{\hskip10.0pt}c}1-\delta & \delta \\{} \delta & 1-\delta \end{array}\right)\alpha ,\]Indeed, notice that $(\begin{array}{c@{\hskip3.33pt}c}1-\delta & \delta \\{} \delta & 1-\delta \end{array})={J}^{\delta }$, and therefore by taking ${\eta ^{\prime }}=\eta +\delta \frac{\pi }{2}[\pi ]$ and
\[ X=R_{\eta }(\alpha _{1}S_{0}\oplus \alpha _{2}S_{\frac{\pi }{2}})=R_{{\eta ^{\prime }}}\big({\alpha ^{\prime }_{1}}S_{0}\oplus {\alpha ^{\prime }_{2}}S_{\frac{\pi }{2}}\big),\]
we can easily prove that ${\eta ^{\prime }}$ is a uniform random variable on $[0,\pi ]$ independent of ${\alpha ^{\prime }}$ (see the proof of Prop. 9), and therefore ${\alpha ^{\prime }}$ is a face length vector of X.Let us consider now the central face length distribution, so let δ be a Bernoulli variable of parameter $\frac{1}{2}$ (i.e., a uniform variable on $\{0,1\}$) independent of α, and let ${\alpha ^{\prime }}={J}^{\delta }\alpha $ be a central face length vector. Then, according to (27),
Consequently, the first- and second-order moments of the face length distribution can be computed as
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \mathbb{E}\big[{\alpha ^{\prime }_{1}}\big]=\mathbb{E}\big[{\alpha ^{\prime }_{2}}\big]=\frac{1}{2}\mathbb{E}[\alpha _{1}+\alpha _{2}],\\{} & \displaystyle \mathbb{E}\big[{{\alpha ^{\prime }_{1}}}^{2}\big]=\mathbb{E}\big[{{\alpha ^{\prime }_{2}}}^{2}\big]=\frac{1}{2}\mathbb{E}\big[{\alpha _{1}^{2}}+{\alpha _{2}}^{2}\big],\\{} & \displaystyle \mathbb{E}\big[{\alpha ^{\prime }_{1}}{\alpha ^{\prime }_{2}}\big]=\mathbb{E}[\alpha _{1}\alpha _{2}].\end{array}\]
Notice that property 10 is well verified,. Indeed, $\mathbb{E}[{\alpha ^{\prime }_{1}}]=\mathbb{E}[{\alpha ^{\prime }_{2}}]=\frac{1}{4}\mathbb{E}[U(X)]$, and the matrix $C[\alpha ]$ is a circulant matrix depending on two parameters.3.3 Characterizing an isotropic regular random zonotope from its Feret diameter random process
We have shown that the distribution of an isotropic random zonotope X can be described by its central face length distribution and studied the properties of such distributions. Here we will show how its characteristics can be connected to the geometrical characteristics of the random zonotope. In particular, we will give formulae that allow us to connect the first- and second-order moments of the Feret diameter of X to those of the central face length distribution.
Let X be an isotropic random zonotope represented by its face length vector α. Let us recall that X can be almost surely expressed as
where η is a uniform random variable independent of $\alpha \ge 0$. Suppose that the condition $\mathbb{E}(U{(X)}^{2})<\infty $ is satisfied. Then, according to Proposition 6, $\alpha \in {L}^{2}({\mathbb{R}_{+}^{N}})$, and the mean and autocovariance of $H_{X}$ exist.
According to Proposition 3, for any representative α of X, some geometrical characteristics of X can be expressed as
Note that $k_{S}$ is a π-periodic function and can be expressed on $[0,\pi ]$ as
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \forall t\in \mathbb{R},\hspace{0.2778em}H_{X}(t)& \displaystyle ={\sum \limits_{i=1}^{N}}\alpha _{i}\big|\sin (t-\eta -\theta _{i})\big|,\\{} \displaystyle U(X)& \displaystyle =2{\sum \limits_{i=1}^{N}}\alpha _{i},\\{} \displaystyle A(X)& \displaystyle =\frac{1}{2}{\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}\alpha _{i}\alpha _{j}\big|\sin (\theta _{i}-\theta _{j})\big|.\end{array}\]
Therefore, by considering $\alpha \in {L}^{2}({\mathbb{R}_{+}^{N}})$ and the independence of α and η, their expectation can be computed by integration with respect to the uniform distribution of η: (28)
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \forall t\in \mathbb{R},\hspace{1em}\mathbb{E}\big[H_{X}(t)\big]& \displaystyle =\frac{2}{\pi }{\sum \limits_{i=1}^{N}}\mathbb{E}[\alpha _{i}],\end{array}\](29)
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathbb{E}\big[U(X)\big]& \displaystyle =2{\sum \limits_{i=1}^{N}}\mathbb{E}[\alpha _{i}],\end{array}\](30)
\[\begin{array}{r@{\hskip0pt}l}\displaystyle A(X)& \displaystyle =\frac{1}{2}{\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}\mathbb{E}[\alpha _{i}\alpha _{j}]\big|\sin (\theta _{i}-\theta _{j})\big|,\end{array}\](31)
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \forall t,{t^{\prime }}\in \mathbb{R},\hspace{1em}\mathbb{E}\big[H_{X}(t)H_{X}\big(t+{t^{\prime }}\big)\big]& \displaystyle ={\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}\mathbb{E}[\alpha _{i}\alpha _{j}]k_{S}\big({t^{\prime }}+\theta _{i}-\theta _{j}\big),\end{array}\]Using Eq. (31) and the stationarity of $H_{X}$, we have
and by introducing the functional
it follows that
(34)
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \forall t,{t^{\prime }}\in \mathbb{R},\hspace{1em}\mathbb{E}\big[H_{X}(t)H_{X}\big(t+{t^{\prime }}\big)\big]=\mathbb{E}\big[H_{X}(t)H_{X}\big(t-{t^{\prime }}\big)\big],\end{array}\](35)
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \forall t,{t^{\prime }}\in \mathbb{R},\hspace{1em}{\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}\mathbb{E}[\alpha _{i}\alpha _{j}]k_{S}\big({t^{\prime }}+\theta _{i}-\theta _{j}\big)={\sum \limits_{j=1}^{N}}{\sum \limits_{i=1}^{N}}\mathbb{E}[\alpha _{i}\alpha _{j}]k_{S}\big({t^{\prime }}+\theta _{j}-\theta _{i}\big),\end{array}\]Proposition 11.
For any real t, $K(t)$ is a circulant matrix. Furthermore, by denoting $((k_{1}(t),\dots ,k_{N}(t)))$ the first line of $K(t)$, we have $K(t)=\operatorname{Circ}((k_{1}(t),\dots ,k_{N}(t)))$ and $K_{ij}(t)=k_{j}(\theta _{i}+t)$ for $1\le i,j\le N$.
Proof.
Let us show that $K(t)$ is a circulant matrix. For any real t, $t+\theta _{i}-\theta _{j}$ depends only on $i-j$; therefore, $K(t)$ is a Toeplitz matrix. Furthermore, for $1\le i\le N-1$ and $1\le j\le N$, $K_{(i+1)j}(t)=k_{S}(t+\theta _{i}-(\theta _{j}-\frac{\pi }{N}))$, but $(\theta _{j}-\frac{\pi }{N})=\theta _{\sigma (j)}$ where $\sigma (j)=(j-2[N])+1$, and thus $K_{(i+1)j}(t)=K_{i\sigma (j)}$. Therefore, the line index $i+1$ of $K(t)$ is a cyclic permutation of the line index i of $K(t)$, so $K(t)$ is a circulant matrix. Furthermore, $k_{j}(\theta _{i}+t)=k_{S}(t+\theta _{i}-\theta _{j})=K_{ij}(t)$. □
Suppose now that α is a central representative of X. We will show that the first- and second-order moments of the central distribution can be easily expressed from the Feret diameter process.
Theorem 3 (Moments of the central face length distribution).
Let X be an isotropic random zonotope represented by a central face length vector α. Then
where $V[x]$ denotes the vector ${}^{t}(\mathbb{E}[x_{1}x_{1}],\dots ,\mathbb{E}[x_{1}x_{N}])$.
(38)
\[ \forall x\in \mathbb{R}\hspace{1em}\forall i=1,\dots ,N,\hspace{1em}\mathbb{E}[\alpha _{i}]=\frac{\pi }{2N}\mathbb{E}\big[H_{X}(x)\big],\]Proof.
Suppose that α is a central representative of X. Then, according to Proposition 10 and Eq. (28), the first-order moment of the central distribution can be expressed as
By Propositions 11 and 10, it follows that $\mathbb{E}[\alpha _{i}\alpha _{j}]=V[\alpha ]_{j-i[N]+1}$ and $K_{ij}(t)=k_{j-i[N]+1}$. Then, for all $t\in \mathbb{R}$,
Note that $V[{H_{X}^{(N)}}]={}^{t}(\mathbb{E}[H_{X}(0)H_{X}(\theta _{1})],\dots \mathbb{E}[H_{X}(0)H_{X}(\theta _{N})])$. Since for $1\le i\le N$, $V[{H_{X}^{(N)}}]_{i}=N{\sum _{s=1}^{N}}V[\alpha ]_{s}k_{s}(\theta _{i})=N{\sum _{s=1}^{N}}V[\alpha ]_{s}K_{is}(0)$, we have that
It is easy to see that $K(0)$ is a symmetric positive definite matrix. Indeed, for $1\le i,j\le N$, $K_{ij}(0)=k_{S}(\theta _{i}-\theta _{j})=k_{S}(\theta _{j}-\theta _{i})=K_{ji}(0)$, and this $K(0)$ is a symmetric matrix. Furthermore, for all $x\in {\mathbb{R}}^{N}$,
(40)
\[ \forall x\in \mathbb{R}\hspace{1em}\forall i=1,\dots ,N,\hspace{1em}\mathbb{E}[\alpha _{i}]=\frac{\pi }{2N}\mathbb{E}\big[H_{X}(x)\big].\](41)
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \mathbb{E}\big[H_{X}(0)H_{X}(t)\big]={\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}\mathbb{E}[\alpha _{i}\alpha _{j}]K_{ij}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}V[\alpha ]_{j-i[N]+1}k_{j-i[N]+1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{i}}V[\alpha ]_{j-i[N]+1}k_{j-i[N]+1}(t)+{\sum \limits_{i=1}^{N}}{\sum \limits_{j=i}^{N}}V[\alpha ]_{j-i[N]+1}k_{j-i[N]+1}(t)\\{} & \displaystyle \hspace{2em}-{\sum \limits_{i=1}^{N}}V[\alpha ]_{1}k_{1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{s=0}^{i-1}}V[\alpha ]_{s+1}k_{s+1}(t)+{\sum \limits_{i=1}^{N}}{\sum \limits_{s=0}^{N-i}}V[\alpha ]_{s+1}k_{N-s[N]+1}(t)-NV[\alpha ]_{1}s_{1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{s=0}^{i-1}}V[\alpha ]_{s+1}k_{s+1}(t)+{\sum \limits_{i=1}^{N}}{\sum \limits_{z=N}^{i}}V[\alpha ]_{N-z+1}k_{z[N]+1}(t)-NV[\alpha ]_{1}k_{1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{s=0}^{i-1}}V[\alpha ]_{s+1}k_{s+1}(t)+{\sum \limits_{i=1}^{N}}{\sum \limits_{z=N}^{i}}V[\alpha ]_{z[N]+1}k_{z[N]+1}(t)-NV[\alpha ]_{1}k_{1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{s=0}^{i-1}}V[\alpha ]_{s+1}k_{s+1}(t)+{\sum \limits_{i=1}^{N}}{\sum \limits_{s=i}^{N}}V[\alpha ]_{s[N]+1}k_{s[N]+1}(t)-NV[\alpha ]_{1}k_{1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{s=0}^{i-1}}V[\alpha ]_{s+1}k_{s+1}(t)+{\sum \limits_{i=1}^{N}}{\sum \limits_{s=i}^{N}}V[\alpha ]_{s[N]+1}k_{s[N]+1}(t)-NV[\alpha ]_{1}k_{1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{s=0}^{N}}V[\alpha ]_{s[N]+1}k_{s[N]+1}(t)-NV[\alpha ]_{1}k_{1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{s=0}^{N-1}}V[\alpha ]_{s[N]+1}k_{s[N]+1}(t)+{\sum \limits_{i=1}^{N}}V[\alpha ]_{1}k_{1}(t)-NV[\alpha ]_{1}k_{1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{s=0}^{N-1}}V[\alpha ]_{s+1}k_{s+1}(t)\\{} & \displaystyle \hspace{1em}={\sum \limits_{i=1}^{N}}{\sum \limits_{s=1}^{N}}V[\alpha ]_{s}k_{s}(t)\\{} \displaystyle \Rightarrow & \displaystyle \hspace{1em}\mathbb{E}\big[H_{X}(0)H_{X}(t)\big]=N{\sum \limits_{s=1}^{N}}V[\alpha ]_{s}k_{s}(t).\end{array}\]
\[\begin{array}{r@{\hskip0pt}l}\displaystyle {}^{t}xK(0)x& \displaystyle ={\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}x_{i}x_{j}K_{ij}(0)\\{} & \displaystyle ={\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}x_{i}x_{j}\frac{1}{\pi }{\int _{0}^{\pi }}\big|\sin (\theta _{i}-\theta _{j}+z)\sin (z)\big|\hspace{0.1667em}dz\\{} & \displaystyle =\frac{1}{\pi }{\int _{0}^{\pi }}{\sum \limits_{i=1}^{N}}{\sum \limits_{j=1}^{N}}x_{i}x_{j}\big|\sin (z-\theta _{i})\sin (z-\theta _{j})\big|\hspace{0.1667em}dz\\{} & \displaystyle =\frac{1}{\pi }{\int _{0}^{\pi }}{\Bigg({\sum \limits_{i=1}^{N}}x_{i}\big|\sin (z-\theta _{i})\big|\Bigg)}^{2}\hspace{0.1667em}dz.\end{array}\]
Denote by Y the real-valued random variable $Y={\sum _{i=1}^{N}}x_{i}|\sin (z-\theta _{i})|$, where z is a uniform random variable on $[0,\pi ]$. Then ${}^{t}xK(0)x=\mathbb{E}[{Y}^{2}]$, and so ${}^{t}xK(0)x\ge 0$. Furthermore, ${}^{t}xK(0)x=0$ if and only if $Y=0$ almost surely, $Y=0$ a.s. $\Rightarrow \forall z\in [0,\pi ]$, and ${\sum _{i=1}^{N}}x_{i}|\sin (z-\theta _{i})|=0\Rightarrow x=0$. Finally, $K(0)$ is a symmetric positive definite matrix. Then it is invertible, and it follows that
□This theorem gives the first- and second-order moments of the central face length distribution from those of the Feret diameter. Note that $V[\alpha ]$ and $V[{H_{X}^{(N)}}]$ satisfy the properties of symmetry. Indeed, by denoting $m=\lfloor \frac{N}{2}\rfloor $ we have shown that if N is an even integer, then $V[\alpha ]={}^{t}(v_{0},\dots ,v_{m-1},v_{m},v_{m-1},\dots ,v_{1})$ and if N is an odd integer, then $V[\alpha ]={}^{t}(v_{0},\dots ,v_{m},v_{m},\dots ,v_{1})$, where $v_{k}=\mathbb{E}[\alpha _{1}\alpha _{1+k}]$, $k=0,\dots ,m$. The vector $V[{H_{X}^{(N)}}]$ can be expressed in the same way: for $i=1,\dots ,N$, $\pi -\theta _{i}=\frac{N-i+2-1}{N}\pi =\theta _{N-i+1[N]+1}$, and
\[\begin{array}{r@{\hskip0pt}l}\displaystyle V\big[{H_{X}^{(N)}}\big]_{i}& \displaystyle =\mathbb{E}\big[H_{X}(0)H_{X}(\theta _{i})\big]\\{} & \displaystyle =\mathbb{E}\big[H_{X}(0)H_{X}(\pi -\theta _{i})\big]\\{} & \displaystyle =V\big[{H_{X}^{(N)}}\big]_{N-i+1[N]+1}.\end{array}\]
Therefore, if N is an even integer, then $V[{H_{X}^{(N)}}]={}^{t}(c_{0},\dots ,c_{m-1},c_{m},c_{m-1},\dots ,v_{1})$, and if N is an odd integer, then $V[{H_{X}^{(N)}}]={}^{t}(c_{0},\dots ,c_{m},c_{m},\dots ,c_{1})$, where $c_{k}=V[{H_{X}^{(N)}}]_{k+1}$, $k=0,\dots ,m$. In practice, the vector $V[\alpha ]$ can be computed by the knowledge of the $m+1$ first components of $V[{H_{X}^{(N)}}]$, and the linear problem (42) can be rewritten and solved as a linear problem of size $m+1$.Remark 5.
In practice, the estimation of $\mathbb{E}[H_{X}(0)H_{X}(t)]$ for $t\in [0,\pi ]$ is often noised. Then, a better choice it is to find $V[\alpha ]$ in the least squares sense. Let ${N^{\prime }}\ge m+1$, and let $0=t_{1}\le \cdots \le t_{{N^{\prime }}}=\frac{\pi }{2}$ be a subdivision of $[0,\pi ]$ containing $\{\theta _{1},\dots ,\theta _{m+1}\}$, the $(t_{i})_{1\le i\le {N^{\prime }}}$ are observation points. Let us recall that for all $t\in [0,\frac{\pi }{2}]$, $\mathbb{E}[H_{X}(0)H_{X}(t)]=\mathbb{E}[H_{X}(0)H_{X}(\pi -t)]$. Then we can suppose that there exist $2({N^{\prime }}-1)$ points of observation such that $z_{i}=t_{i}$ for $i=1,\dots ,{N^{\prime }}$ and $z_{i}=t_{2{N^{\prime }}-i}$ for $i={N^{\prime }}+1,\dots ,2{N^{\prime }}-2$. Let $Q_{ij}=k_{j}(z_{i})$ and $V[{H_{X}^{(2({N^{\prime }}-1))}}]={}^{t}(\mathbb{E}[H_{X}(0)H_{X}(z_{1})],\dots ,\mathbb{E}[H_{X}(0)H_{X}(z_{2({N^{\prime }}-1))}])$. Then, by (41),
Finally, if $\hat{V}[{H_{X}^{(2({N^{\prime }}-1))}}]$ is a noisy estimation of $V[{H_{X}^{(2({N^{\prime }}-1))}}]$, then the following least square estimator of $V[\alpha ]$ is better than that provided by (39):
We have discussed some properties of the random zonotopes. The 0-regular random zonotopes and the regular random zonotope were defined and studied. We have shown that a 0-regular random zonotope can be describes by a unique face length distribution. Such a distribution can be easily related to the Feret diameter of the 0-regular random zonotope by the relations established in Section 1.
We have studied different face length distributions of a regular random zonotope. We have shown that, among them, one can be identified, the central face length distribution. Finally, we have given some formulae that allow us to compute the first- and second-order moments of the central face length distribution from those of the Feret diameter of the regular random zonotope. The following section is devoted to a description of a random symmetric convex set as a 0-regular random zonotope and as a regular random zonotope.
4 Description of a random symmetric convex set as a random zonotope from its Feret diameter
In Section 1, we have defined some approximations of a symmetric convex set as zonotopes. In Section 2, we characterized the regular and 0-regular random zonotopes from their Feret diameters random process. The aim of this section is to generalize the previous approximations to a random symmetric convex set X.
Firstly, we will show that the 0-regular random zonotope corresponding to the ${\mathcal{C}_{0}^{(N)}}$-approximation of X can be characterized from the Feret diameter random process of X. Secondly, we will show that the isotropic regular random zonotope corresponding to the ${\mathcal{C}_{\infty }^{(N)}}$-approximation of an isotropized set of X can be estimated from the Feret diameter random process of X.
4.1 Approximation of a random symmetric convex set by a 0-regular random zonotope
Here we investigate the approximation of a random symmetric convex set X by a 0-regular random zonotope. We show that the random set ${X_{0}^{(N)}}$ valued in ${\mathcal{C}_{0}^{(N)}}$ that is defined as the ${\mathcal{C}_{0}^{(N)}}$-approximation of realizations of X can be characterized from the Feret diameter of X. Finally, we give some formulas that allow us to compute the moments of the random vector of the faces of ${X_{0}^{(N)}}$.
Proposition 12 (Approximation by a 0-regular random zonotope).
Let X be a random convex set. For any $\omega \in \varOmega $ a.s., let ${X_{0}^{(N)}}(\omega )$ be the ${\mathcal{C}_{0}^{(N)}}$-approximation of $X(\omega )$. The 0-regular random zonotope ${X_{0}^{(N)}}$ is called the ${\mathcal{C}_{0}^{(N)}}$-approximation of the random set X.
For any $N>1$, an interval of confidence for the Hausdorff distance can be built. Indeed, for any $a>0$, we have the relation
If $\epsilon \in [0,1]$ is a confidence level, then $a(\epsilon ,N)=\frac{(6+2\sqrt{2})}{\epsilon }\sin (\frac{\pi }{2N})\mathbb{E}[\operatorname{diam}(X)]$ can be considered as an upper bound for $d_{H}(X,{X_{0}^{(N)}})$ with confidence $1-\epsilon $.
(44)
\[ \mathbb{P}\big(d_{H}\big(X,{X_{0}^{(N)}}\big)>a\big)\le \frac{(6+2\sqrt{2})}{a}\sin \bigg(\frac{\pi }{2N}\bigg)\mathbb{E}\big[\operatorname{diam}(X)\big].\]
Consequently, such an approximation is consistent as $N\to \infty $.
Proof.
Let X be a random convex set. For any $\omega \in \varOmega $ a.s., let ${X_{0}^{(N)}}(\omega )$ be the ${\mathcal{C}_{0}^{(N)}}$-approximation of $X(\omega )$ in ${\mathcal{C}_{0}^{(N)}}$. According to Theorem 3, for any real $a>0$,
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \forall \omega \in \varOmega \hspace{2.5pt}\text{a.s.},\hspace{1em}d_{H}\big(X,{X_{0}^{(N)}}\big)\le (6+2\sqrt{2})\sin \bigg(\frac{\pi }{2N}\bigg)\operatorname{diam}(X)\\{} \displaystyle \Rightarrow \hspace{1em}& \displaystyle \mathbb{P}\big(d_{H}\big(X,{X_{0}^{(N)}}\big)>a\big)\le \mathbb{P}\bigg((6+2\sqrt{2})\sin \bigg(\frac{\pi }{2N}\bigg)\operatorname{diam}(X)>a\bigg).\end{array}\]
By using the Markov inequality [9] it follows that
\[ \mathbb{P}\big(d_{H}\big(X,{X_{0}^{(N)}}\big)>a\big)\le \frac{(6+2\sqrt{2})}{a}\sin \bigg(\frac{\pi }{2N}\bigg)\mathbb{E}\big[\operatorname{diam}(X)\big].\]
The consistence of the approximation as $N\to \infty $ follows directly from this relation. □According to relation (16), $\mathbb{E}[\operatorname{diam}(X)]$ can be replaced by $\frac{1}{2}\mathbb{E}[U(X)]$.
Let X be a random symmetric convex set, and ${X_{0}^{(N)}}$ be its ${\mathcal{C}_{0}^{(N)}}$-approximation. The, in the same way as in the deterministic case, the face length distribution can be related to the Feret diameter of X.
Proposition 13 (Characterization of the ${\mathcal{C}_{0}^{(N)}}$-approximation from the Feret diameter process).
Let $N>1$ be an integer, and X be a random symmetric convex set. Let ${X_{0}^{(N)}}$ be the ${\mathcal{C}_{0}^{(N)}}$-approximation of X. Its face length vector α can be characterized from the Feret diameter process:
where ${H_{X}^{(N)}}={}^{t}(H_{X}(\theta _{1}),\dots ,H_{X}(\theta _{1}))$ is the random vector composed by the Feret diameter evaluated on the regular subdivision. The matrix ${F}^{(N)}$ is still defined as $(|\sin (\theta _{i}-\theta _{j})|)_{ij})_{1\le i,j\le N}$, and for a vector x, $C[x]$ denotes its second-order moments $\mathbb{E}[x{}^{t}x]$.
(45)
\[ \forall \omega \in \varOmega \textit{a.s.}\hspace{1em}\alpha (\omega )={{F}^{(N)}}^{-1}{H_{X}^{(N)}}(\omega ),\]Proof.
According to Theorem 3, the matrix ${F}^{(N)}$ is invertible, and thus by the definition of the approximation relation (45) follows. Noting that $\alpha {}^{t}\alpha ={{F}^{(N)}}^{-1}{H_{X}^{(N)}}{}^{t}{H_{X}^{(N)}}{}^{t}{{F}^{(N)}}^{-1}$, relations (46) and (47) follow from the linearity of the expectation. □
Remark 6.
The ${\mathcal{C}_{0}^{(N)}}$-approximation of a random symmetric convex set X is a consistent approximation as $N\to \infty $. Furthermore, if X is already a 0-regular random zonotope in ${\mathcal{C}_{0}^{(N)}}$, then its Mth approximation ${X_{0}^{(M)}}$ coincides with X if and only if N is a divider of M.
Such an approximation is sensitive to a rotation of X. Indeed, if $R_{\eta }(X)$ is the rotation of X by the random angle η, then the random sets X and $R_{\eta }(X)$ have different approximations. This property can be seen as an advantage or a disadvantage. Indeed, if the objective is to describe the direction of some random set, then it is an advantage, but there is a need to use large N. However, when the objective is to describe the shape of a random set with a small N without taking into consideration its direction, then it can be a great disadvantage; see the following example.
Example 3.
Let $N=2$, and let $\theta _{1}=0$, $\theta _{2}=\frac{\pi }{2}$, the regular subdivision. Let us consider the random symmetric convex set X as a deterministic square of side 1, that is, $X=S_{\theta _{1}}\oplus S_{\theta _{2}}$. Its ${\mathcal{C}_{0}^{(2)}}$-approximation coincides with X: ${X_{0}^{(2)}}=X$. The matrix ${F}^{(N)}$ is defined as
\[ {F}^{(N)}={{F}^{(N)}}^{-1}=\left(\begin{array}{c@{\hskip10.0pt}c}0& 1\\{} 1& 0\end{array}\right),\]
and, consequently,
\[ \mathbb{E}[\alpha _{X}]=\left(\begin{array}{c}1\\{} 1\end{array}\right),\hspace{1em}C[\alpha _{X}]=\left(\begin{array}{c@{\hskip10.0pt}c}1& 1\\{} 1& 1\end{array}\right)\hspace{2.5pt}\text{and}\hspace{2.5pt}\operatorname{Cov}(\alpha _{X})=0.\]
Consider now the random symmetric convex set $Y=R_{\eta }(X)$ where η is a uniform random variable on $[0,\pi ]$. Then the mean and covariance of its Feret diameter can be computed (see (31) to (33)):
\[ \mathbb{E}\big[{H_{Y}^{(N)}}\big]=\left(\begin{array}{c}\frac{4}{\pi }\\{} \frac{4}{\pi }\end{array}\right)\hspace{2.5pt}\text{and}\hspace{2.5pt}C\big[{H_{Y}^{(N)}}\big]=\bigg(1+\frac{2}{\pi }\bigg)\left(\begin{array}{c@{\hskip10.0pt}c}1& 1\\{} 1& 1\end{array}\right).\]
So
\[ \mathbb{E}[\alpha _{Y}]=\frac{4}{\pi }\left(\begin{array}{c}1\\{} 1\end{array}\right),\hspace{1em}C[\alpha _{Y}]=\bigg(\frac{\pi +2}{\pi }\bigg)\left(\begin{array}{c@{\hskip10.0pt}c}1& 1\\{} 1& 1\end{array}\right),\]
and
\[ \operatorname{Cov}(\alpha _{Y})=\frac{{\pi }^{2}+2\pi -16}{{\pi }^{2}}\left(\begin{array}{c@{\hskip10.0pt}c}1& 1\\{} 1& 1\end{array}\right).\]
The random set Y is approximated by a random rectangle that has a varying sides $(\operatorname{Cov}(\alpha _{Y})\ne 0)$. However, Y have the same geometrical shape as X. This example shows that the ${\mathcal{C}_{0}^{(N)}}$-approximation cannot be used to describe the shape of a random symmetric convex set for small N.In order to describe the shape of a random symmetric convex set as a zonotope with a small number of faces, we need to have an approximation insensitive to the rotations. This leads us to the following approximation.
4.2 Approximation of a random symmetric convex set by an isotropic random zonotope
Previously, we have shown that a random symmetric convex set can be approximated as a random 0-regular zonotope. However, we have also shown that such an approximation can be problematic for small values of N. The aim of this section is to define and characterize an approximation in ${\mathcal{C}_{\infty }^{(N)}}$ that is invariant up to a rotation and that can be used for not so large N. For this objective, we give the approximation for an isotropized set of X instead of X. We will show that a random symmetric convex set can be approximated up to a rotation by an isotropic random regular zonotope.
Let us note $Y=R_{z}(X)$ the isotropized set of X with z an independent uniform variable on $[0,\pi ]$. Let ${X_{\infty }^{(N)}}$ be a ${\mathcal{C}_{\infty }^{(N)}}$-approximation of X. Then
\[ \forall \omega \in \varOmega \hspace{2.5pt}\text{a.s.},\hspace{1em}{X_{\infty }^{(N)}}(\omega )=R_{\tau (\omega )}\big({\tilde{X}_{0}^{(N)}}(\omega )\big).\]
According to the definition of the ${\mathcal{C}_{\infty }^{(N)}}$-approximation, the random set ${Y_{\infty }^{(N)}}=R_{z}({X_{\infty }^{(N)}})$ is a ${\mathcal{C}_{\infty }^{(N)}}$-approximation of Y. Consequently, ${Y_{\infty }^{(N)}}=R_{z+\tau }({\tilde{X}_{0}^{(N)}})$. Because of the independence of η and X, by the property of addition modulo π the random variable $\eta =z+\tau $ is a uniform random variable on $[0,\pi ]$ independent of X. Then ${Y_{\infty }^{(N)}}$ is an isotropic regular zonotope. We will use such a random regular zonotope as the approximation of X up to a rotation.Definition 11 (${\mathcal{C}_{\infty }^{(N)}}$-isotropic approximation).
Let X be a random symmetric convex set, and $Y=R_{z}(X)$ its isotropized set. The isotropic random regular zonotope ${Y_{\infty }^{(N)}}=R_{z}({X_{\infty }^{(N)}})$ is called the ${\mathcal{C}_{\infty }^{(N)}}$-isotropic approximation of X and denoted by ${\tilde{X}_{\infty }^{(N)}}$.
Proposition 14 (Properties of the ${\mathcal{C}_{\infty }^{(N)}}$-isotropic approximation).
Let X be a random symmetric convex set, and ${\tilde{X}_{\infty }^{(N)}}$ be its ${\mathcal{C}_{\infty }^{(N)}}$-isotropic approximation.
-
1. ${\tilde{X}_{\infty }^{(N)}}$ is an isotropic random regular zonotope.
-
2. $\forall \omega \in \varOmega $ a.s., $\exists t(\omega )\in [0,\pi ]$, $\forall i=1,\dots ,N$, $H_{X}(t+\theta _{i})=H_{{\tilde{X}_{\infty }^{(N)}}}(t+\theta _{i})$.
-
3. $\forall \omega \in \varOmega $ a.s., $d_{P}(X,{Y_{\infty }^{(N)}})\to 0$ as $N\to \infty $.
-
4. The ${\mathcal{C}_{\infty }^{(N)}}$-isotropic approximation is invariant up to a rotation of X.
-
5. If X is a random regular zonotope, then any face length vector of ${\tilde{X}_{\infty }^{(N)}}$ is a face length vector of X.
Proof.
$\hspace{0.2222em}$
□
-
1. It is easy to see that ${\tilde{X}_{\infty }^{(N)}}$ is an isotropized set of ${X_{\infty }^{(N)}}$. Consequently, it is an isotropic random regular zonotope.
-
2–4. These properties are direct consequences of Theorem 2.
-
5. Suppose that X is a random regular zonotope. Then X and ${\tilde{X}_{\infty }^{(N)}}$ coincide up to a random rotation, and any face length vector of the one is a face length vector of the other one.
In order to describe the shape of X, the best way would be to characterize the central face length distribution of ${\tilde{X}_{\infty }^{(N)}}$ from information available on X. Unfortunately, there is no way to compute the characteristics of the random process $H_{{\tilde{X}_{\infty }^{(N)}}}$ from those of $H_{X}$. However, the approximation of the first- and second-order moments of $H_{{\tilde{X}_{\infty }^{(N)}}}$ can be estimated from those of the Feret diameters of an isotropized set of X (i.e., $H_{Y}$, where Y is an isotropized set of X).
Proposition 15 (Approximation of the moments of the central face length distribution).
Let X be a symmetric random convex set, Y its isotropized set, ${\tilde{X}_{\infty }^{(N)}}$ the ${\mathcal{C}_{\infty }^{(N)}}$-isotropic approximation of X, and α the central face length vector of ${\tilde{X}_{\infty }^{(N)}}$.
-
1. An approximation of the first- and second-order moments of α is given by Such an approximation is consistent as $N\to \infty $: $\hat{\mathbb{E}}[\alpha ]-\mathbb{E}[\alpha ]\to 0$ and $\hat{V}[\alpha ]-V[\alpha ]\to 0$ as $N\to \infty $.
-
2. If $\hat{\alpha }$ is a positive random vector satisfying $V[\hat{\alpha }]=\hat{V}[\alpha ]$, $\mathbb{E}[\hat{\alpha }]=\hat{\mathbb{E}}[\alpha ]$, and η an independent uniform variable on $[0,\pi ]$, then the random set $\hat{X}$ defined assatisfies $\mathbb{E}[U(X)]=\mathbb{E}[U(\hat{X})]$.
(50)
\[ \hat{X}=R_{\eta }\Bigg({\underset{i=1}{\overset{N}{\bigoplus }}}\hat{\alpha }_{i}S_{\theta _{i}}\Bigg)\]
Proof.
$\hspace{0.2222em}$
□
-
1. The consistence of the estimate is trivial regarding that $\mathbb{E}[{H_{Y}^{(N)}}]\to \mathbb{E}[{H_{{\tilde{X}_{\infty }^{(N)}}}^{(N)}}]$ and $V[{H_{Y}^{(N)}}]\to V[{H_{{\tilde{X}_{\infty }^{(N)}}}^{(N)}}]$ as $N\to \infty $.
-
2. Let $\hat{\alpha }$ be a positive random vector satisfying $V[\hat{\alpha }]=\hat{V}[\alpha ]$, $\mathbb{E}[\hat{\alpha }]=\hat{\mathbb{E}}[\alpha ]$, and η an independent uniform variable on $[0,\pi ]$. Because of the isotropy of Y, the vector $\mathbb{E}[{H_{Y}^{(N)}}]$ has all its components equal to $\frac{1}{\pi }\mathbb{E}[(U(Y)]$, and the random set $\hat{X}=R_{\eta }({\bigoplus _{i=1}^{N}}\hat{\alpha }_{i}S_{\theta _{i}})$ satisfies
Remark 7.
Firstly, note that the quantities $\mathbb{E}[{H_{Y}^{(N)}}]$ and $V[{H_{Y}^{(N)}}]$ are easily obtained from the mean and autocovariance of $H_{X}$ by using property 4. The approximations $\hat{\mathbb{E}}[\alpha ]$ and $\hat{V}[\alpha ]$ can be regarded as the characteristics of the central face length vector of an isotropic random regular zonotope $\hat{X}$, which has the same Feret diameter on the $\theta _{i}$ as an isotropized set of X. In particular, such a zonotope has the same mean perimeter as X.
Furthermore, if X is an Nth random regular zonotope, then such quantities coincide with those of a face length vector of X. Consequently it is more interesting to use the ${\mathcal{C}_{\infty }^{(N)}}$-isotropic approximation when X is assumed to be an Nth random regular zonotope.
5 Conclusions and prospects
In this paper, we proposed different approximations of a symmetric convex set as a zonotope. These approximations have been further generalized to random symmetric convex sets. We have shown that a random convex set can be approximated as precisely as we want as a random zonotope in terms of the Hausdorff distance. More specifically, for a random symmetric convex set X, the first- and second-order moments of the face length vector of its zonotope approximation can be computed from the first- and second-order moments of the Feret diameter process of X.
This work involves several perspectives. The first one would be to get higher moments of the central face length distribution and to generalize this work in higher dimension. One potential application of this work would be to describe the primary grain of the germ–grain model. Indeed, in a large class of such models, there exist estimators for the moments of the Feret diameter of the primary grain [25]. In particular, we prospect to apply this to the images of oxalate ammonium crystals modeled by the Boolean model (see [25, 26]). However, we need to study the estimators involved by the zonotope approximation in those germ–grain models.

