1 Introduction
Integrated distribution and quantile functions or simple transformations of them play an important role in probability theory, mathematical statistics, and their applications such as insurance, finance, economics etc. They frequently appear in the literature, often under different names. Moreover, in many occasions they are defined under additional assumption of integrability of a random variable or at least integrability of the positive or the negative part of a variable. Let us point out only few references. For a random variable X, let $F_{X}$ be the distribution function of X and $q_{X}$ any quantile function of X. Examples of integrated distribution functions or their simple modifications are:
These transforms characterize the distribution of X only if the expectations $\mathsf{E}{X}^{-}$, or $\mathsf{E}{X}^{+}$, or $\mathsf{E}|X|$ respectively are finite; otherwise, the transforms equal $+\infty $ or $-\infty $ identically and do not allow to identify the distribution of X.
-
• The functionconsidered in [11].
(1)
\[ \varPsi _{X}(x):={\int _{-\infty }^{x}}F_{X}(t)\hspace{0.1667em}dt,\hspace{1em}x\in \mathbb{R},\]
The examples of integrated quantile functions or their simple transformations are:
Again, these transforms characterize the distribution of X if either $\mathsf{E}[{X}^{-}]<\infty $ or $\mathsf{E}[{X}^{+}]<\infty $, otherwise, they are equal to $+\infty $ or $-\infty $ identically.
-
• The absolute Lorenz curvesee, e.g., [21] and the references therein.
(4)
\[ \operatorname{AL}_{X}(u):={\int _{0}^{u}}q_{X}(s)\hspace{0.1667em}ds,\hspace{1em}u\in [0,\hspace{0.1667em}1],\] -
• The Hardy–Littlewood maximal functionof X, see [14].
(5)
\[ \operatorname{HL}_{X}(u):=\frac{1}{1-u}{\int _{u}^{1}}q_{X}(s)\hspace{0.1667em}ds,\hspace{1em}u\in [0,\hspace{0.1667em}1),\]
The main goal of this paper is a systematic exposition of basic properties of integrated distribution and quantile functions. In particular, we define the integrated distribution and quantile functions for any random variable X in such a way that each one of these functions determines uniquely the distribution of X. Further, we show that such important notions of probability theory as uniform integrability, weak convergence and tightness can be characterized in terms of integrated quantile functions (see Section 3). In Section 4 we show how some basic results of the theory of comparison of binary statistical experiments can be deduced using our results in previous two sections. Finally, in Section 5 we extend the area of application of the Chacon–Walsh construction in the Skorokhod embedding problem with the help of integrated quantile functions.
One of the key points of our approach is that we define integrated distribution and quantile functions as Fenchel conjugates of each other. This is due to the fact that their derivatives, distribution functions and quantile functions, are generalized inverses (see, e. g., [8, 11]). This convex duality result can be found in [21] and [11, Lemma A.26], and constitutes implicitly one of two main results in [22, 23].
Let us note that we consider only univariate distributions in this paper. However, it is reasonable to mention a possible generalization to the multidimensional case based on ideas from optimal transport. The integrated quantile function of a random variable X, as it is defined in our paper, is a convex function whose gradient pushes forward the uniform distribution on $(0,\hspace{0.1667em}1)$ into the distribution of X; moreover, the integrated distribution function is the Fenchel transform of the integrated quantile function and its gradient pushes forward the distribution of X into the uniform distribution on $(0,\hspace{0.1667em}1)$ if the distribution of X is continuous. It the multidimensional case the existence of such functions follows from the McCann theorem [18]. Namely, if μ is the distribution on ${\mathbb{R}}^{d}$, then there exists a (unique up to an additive constant) convex function V whose gradient pushes forward the uniform distribution on the unit cube (or, say, the unit ball) in ${\mathbb{R}}^{d}$ into μ. Additionally, if μ vanishes on Borel subsets of Hausdorff dimension $d-1$, then the Fenchel transform ${V}^{\ast }$ of V pushes forward μ to the corresponding uniform distribution. We refer to [3, 5, 9] and [13] for recent advances in this area.
It is more convenient for us to speak about random variables rather than distributions. However, if a probability space is not specified, the symbols $\mathsf{P}$ and $\mathsf{E}$ for probability and expectation enter into consideration only via distributions of random variables and may refer to different probability spaces. This allows us to replace occasionally random variables by their distributions in the notation.
For the reader’s convenience, we recall some terminology and elementary facts concerning convex functions of one real variable. A convex function $f:\mathbb{R}\to \mathbb{R}\cup \{+\infty \}$ is proper if its effective domain
is not empty. The subdifferential $\partial f(x)$ of f at a point x is defined by
\[ \partial f(x)=\big\{u\in \mathbb{R}:f(y)\ge f(x)+u(y-x)\hspace{2.5pt}\text{for every}\hspace{2.5pt}y\in \mathbb{R}\big\}.\]
If f is a proper convex function and x is an interior point of $\operatorname{dom}f$, then $\partial f(x)=[{f^{\prime }_{-}}(x),{f^{\prime }_{+}}(x)]$, where ${f^{\prime }_{-}}(x)$ and ${f^{\prime }_{+}}(x)$ are the left and right derivatives of f at x respectively. The conjugate of f, or the Fenchel transform, is the function ${f}^{\ast }$ on $\mathbb{R}$ defined by
The conjugate function is lower semicontinuous and convex. The Fenchel–Moreau theorem says that if f is a proper lower semicontinuous convex function, then f is the conjugate of ${f}^{\ast }$, i.e.
moreover, for $x,u\in \mathbb{R}$,
2 Integrated distribution and quantile functions: definitions and main properties
2.1 Definition and properties of integrated distribution functions
The distribution function $F_{X}$ of a random variable X given on a probability space $(\varOmega ,\hspace{0.1667em}\mathcal{F},\hspace{0.1667em}\mathsf{P})$ is defined by $F_{X}(x)=\mathsf{P}(X\le x)$, $x\in \mathbb{R}$. Since $F_{X}$ is bounded, for any choice of $x_{0}\in \mathbb{R}$, the integral ${\int _{x_{0}}^{x}}F_{X}(t)\hspace{0.1667em}dt$ is defined and finite for all $x\in \mathbb{R}$.2 In contrast to this case, the function $\varPsi _{X}$ in (1) corresponding to the choice $x_{0}=-\infty $, takes value $+\infty $ identically if $\mathsf{E}[{X}^{-}]=\infty $.
Theorem 1.
An integrated distribution function $\mathsf{J}_{X}$ has the following properties:
-
(i) $\mathsf{J}_{X}(0)=0$.
-
(ii) $\mathsf{J}_{X}$ is convex, increasing and finite everywhere on $\mathbb{R}$.
-
(iv) $\underset{x\to -\infty }{\lim }\mathsf{J}_{X}(x)=-\mathsf{E}[{X}^{-}]$ and $\underset{x\to +\infty }{\lim }(x-\mathsf{J}_{X}(x))=\mathsf{E}[{X}^{+}]$.
-
(v) $\underset{x\to -\infty }{\lim }\frac{\mathsf{J}_{X}(x)}{x}=0$ and $\underset{x\to +\infty }{\lim }\frac{\mathsf{J}_{X}(x)}{x}=1$.
-
(vii) $\mathsf{J}_{-X}(x)=x+\mathsf{J}_{X}(-x)$ for all $x\in \mathbb{R}$.
It is clear from (vi), that the integrated distribution function uniquely determines the distribution.
Proof.
It is evident that (i) holds and $\mathsf{J}_{X}$ is finite and increasing. For $a<b$, we have
It follows that, for any $x,\hspace{0.1667em}y\in \mathbb{R}$,
if $p\in [F_{X}(x-0),\hspace{0.1667em}F_{X}(x)]$. Now the convexity of $\mathsf{J}_{X}$ follows, which, in turn, implies (vi).
(10)
\[ F_{X}(a)(b-a)\le \mathsf{J}_{X}(b)-\mathsf{J}_{X}(a)={\int _{a}^{b}}F_{X}(t)\hspace{0.1667em}dt\le F_{X}(b-0)(b-a)\text{.}\]Next, by Fubini’s theorem, for $a<b$,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle {\int _{a}^{b}}F_{X}(t)\hspace{0.1667em}dt& \displaystyle ={\int _{a}^{b}}\mathsf{E}[\mathbb{1}_{\{X\le t\}}]\hspace{0.1667em}dt=\mathsf{E}\Bigg[{\int _{a}^{b}}\mathbb{1}_{\{X\le t\}}\hspace{0.1667em}dt\Bigg]\\{} & \displaystyle =\mathsf{E}\big[{(b-X)}^{+}-{(X-a)}^{-}\big]\text{.}\end{array}\]
Thus, we have proved (7). The second equality in (8) is trivial, and the first one follows from (7) if we put $a=0$ or $b=0$ depending on the sign of x.Let us prove (iv). The function ${(x-X)}^{+}-{X}^{-}$ is increasing in x, hence $\mathsf{E}[{(x-X)}^{+}-{X}^{-}]\to -\mathsf{E}[{X}^{-}]$ as $x\to -\infty $ by the monotone convergence theorem. This proves the first equality in (iv). Similarly, $x-{(x-X)}^{+}+{X}^{-}$ is increasing in x, hence $\mathsf{E}[x-{(x-X)}^{+}+{X}^{-}]\to \mathsf{E}[{X}^{+}]$ as $x\to +\infty $ by the monotone convergence theorem.
Fig. 1.
A typical graph of an integrated distribution function if the expectations $\mathsf{E}[{X}^{-}]$ and $\mathsf{E}[{X}^{+}]$ are finite
Corollary 1.
If X is an integrable random variable, then, for any $x\in \mathbb{R}$,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \varPsi _{X}(x)& \displaystyle =\mathsf{J}_{X}(x)+\mathsf{E}\big[{X}^{-}\big],\\{} \displaystyle H_{X}(x)& \displaystyle =\mathsf{J}_{X}(x)+\mathsf{E}\big[{X}^{+}\big]-x,\\{} \displaystyle U_{X}(x)& \displaystyle =x-\mathsf{E}|X|-2\mathsf{J}_{X}(x),\end{array}\]
where $\varPsi _{X}$, $H_{X}$, and $U_{X}$ are defined in (1)–(3), in particular,
Theorem 2.
If $J:\mathbb{R}\to \mathbb{R}$, $J(0)=0$, is a convex function satisfying
\[ \underset{x\to -\infty }{\lim }\frac{J(x)}{x}=0\hspace{1em}\textit{and}\hspace{1em}\underset{x\to +\infty }{\lim }\frac{J(x)}{x}=1,\]
then there exists on some probability space a random variable X for which $\mathsf{J}_{X}=J$.
Proof.
Since J is convex and finite everywhere on the line, it has the right-hand derivative at each point, and $J(x)={\int _{0}^{x}}{J^{\prime }_{+}}(t)\hspace{0.1667em}dt$. Moreover, similarly to the proof of (v) in Theorem 1, $\lim _{x\to -\infty }{J^{\prime }_{+}}(x)=\lim _{x\to -\infty }\frac{J(x)}{x}=0$ and $\lim _{x\to +\infty }{J^{\prime }_{+}}(x)=\lim _{x\to +\infty }\frac{J(x)}{x}=1$. Put $F(x):={J^{\prime }_{+}}(x)$. Due to convexity of J, F is an increasing and right-continuous function. So we can conclude, that F is the distribution function of some random variable X and $\mathsf{J}_{X}=J$. □
2.2 Definition and properties of integrated quantile functions
We call every function $q_{X}:(0,\hspace{0.1667em}1)\to \mathbb{R}$ satisfying
\[ F_{X}\big(q_{X}(u)-0\big)\le u\le F_{X}\big(q_{X}(u)\big),\hspace{1em}u\in (0,\hspace{0.1667em}1),\]
a quantile function of a random variable X. The functions ${q_{X}^{L}}$ and ${q_{X}^{R}}$ defined by
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle {q_{X}^{L}}(u):=\inf \big\{x\in \mathbb{R}:F_{X}(x)\ge u\big\},\\{} & \displaystyle {q_{X}^{R}}(u):=\inf \big\{x\in \mathbb{R}:F_{X}(x)>u\big\},\end{array}\]
are called the lower (left) and upper (right) quantile functions of X. Of course, the lower and upper quantile functions of X are quantile functions of X, and we always have
for any quantile function $q_{X}$.It follows directly from the definitions that, for any $x\in \mathbb{R}$ and $u\in (0,\hspace{0.1667em}1)$,
See, e. g., [8, 11] for more information on quantile functions (generalized inverses).
This definition is motivated by the fact mentioned in the introduction, that a function whose derivative is a quantile function must coincide with the Fenchel transform of $\mathsf{J}_{X}$ up to an additive constant. The next theorem clarifies this point.
Theorem 3.
An integrated quantile function $\mathsf{K}_{X}$ has the following properties :
-
(i) The function $\mathsf{K}_{X}$ is convex and lower semicontinuous. It takes finite values on $(0,\hspace{0.1667em}1)$ and equals $+\infty $ outside $[0,\hspace{0.1667em}1]$.
-
(iii) $\min _{u\in \mathbb{R}}\mathsf{K}_{X}(u)=0$, $\{u\in \mathbb{R}:\mathsf{K}_{X}(u)=0\}=[F_{X}(0-0),\hspace{0.1667em}F_{X}(0)]$.
-
(v) $\mathsf{K}_{X}(0)=\mathsf{E}[{X}^{-}]$ and $\mathsf{K}_{X}(1)=\mathsf{E}[{X}^{+}]$.
-
(vi) The subdifferential of $\mathsf{K}_{X}$ satisfiesin particular, ${(\mathsf{K}_{X})^{\prime }_{-}}(u)={q_{X}^{L}}(u)$ and ${(\mathsf{K}_{X})^{\prime }_{+}}(x)={q_{X}^{R}}(u)$.
(16)
\[ \partial \mathsf{K}_{X}(u)=\big[{q_{X}^{L}}(u),\hspace{0.1667em}{q_{X}^{R}}(u)\big],\hspace{1em}u\in (0,\hspace{0.1667em}1),\] -
(vii) $\mathsf{K}_{-X}(u)=\mathsf{K}_{X}(1-u)$ for all $u\in [0,\hspace{0.1667em}1]$.
It is clear from (ii) and the similar remark after Theorem 1 that the integrated quantile function uniquely determines the distribution.
Proof.
Since $\mathsf{J}_{X}$ is a proper convex continuous function, it follows from the definition of $\mathsf{K}_{X}$ and the Fenchel–Moreau theorem that $\mathsf{K}_{X}$ is convex and lower semicontinuous, (14) holds, and for all $x,\hspace{0.1667em}u\in \mathbb{R}$
where the last equivalence follows from (9). In particular,
(17)
\[ u\in \partial \mathsf{J}_{X}(x)\hspace{1em}\Leftrightarrow \hspace{1em}x\in \partial \mathsf{K}_{X}(u)\hspace{1em}\Leftrightarrow \hspace{1em}F_{X}(x-0)\le u\le F_{X}(x)\text{,}\]
\[ \partial \mathsf{K}_{X}(u)=\varnothing ,\hspace{1em}\text{if}\hspace{2.5pt}u\notin [0,\hspace{0.1667em}1],\]
and, for $u\in (0,\hspace{0.1667em}1)$,
\[ x\in \partial \mathsf{K}_{X}(u)\hspace{1em}\Leftrightarrow \hspace{1em}{q_{X}^{L}}(u)\le x\le {q_{X}^{R}}(u)\text{,}\]
due to (11) and (12). Thus, we have proved (i), (ii) and (vi).Putting $x=0$ in (14) and (17), we get $\inf _{u\in \mathbb{R}}\mathsf{K}_{X}(u)=0$ and this infimum is attained at u if and only if $u\in [F_{X}(0-0),\hspace{0.1667em}F_{X}(0)]$. This constitutes assertion (iii). Now (iv) follows from preceding statements.
Statement (v) follows from the definition of $\mathsf{K}_{X}$ and Theorem 1 (iv):
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathsf{K}_{X}(0)& \displaystyle =-\underset{x\in \mathbb{R}}{\inf }\mathsf{J}_{X}(x)=-\underset{x\to -\infty }{\lim }\mathsf{J}_{X}(x)=\mathsf{E}\big[{X}^{-}\big]\text{,}\\{} \displaystyle \mathsf{K}_{X}(1)& \displaystyle =\underset{x\in \mathbb{R}}{\sup }\big(x-\mathsf{J}_{X}(x)\big)=\underset{x\to +\infty }{\lim }\big(x-\mathsf{J}_{X}(x)\big)=\mathsf{E}\big[{X}^{+}\big]\text{.}\end{array}\]
Finally, (vii) follows from the definition of $\mathsf{K}_{X}$ and Theorem 1 (vii). □
Proof.
Put $u:=F_{X}(x)$ and $g(y):=\mathsf{J}_{X}(y)-yu$, $y\in \mathbb{R}$. According to (9), $\partial g(y)=[F_{X}(y-0)-u,\hspace{0.1667em}F_{X}(y)-u]$, in particular, $0\in \partial g(y)$ if $y=x$. This means that the function g attains its minimum at x and, hence, we have $\mathsf{K}_{X}(u)=\sup _{y\in \mathbb{R}}\{yu-\mathsf{J}_{X}(y)\}=xu-\mathsf{J}_{X}(x)$. □
Theorem 4.
If a convex lower semicontinuous function $K:\mathbb{R}\to \mathbb{R}_{+}\cup \{+\infty \}$ satisfies
and there is $u_{0}\in [0,\hspace{0.1667em}1]$ such that $K(u_{0})=0$, then there exists on some probability space a random variable X for which $\mathsf{K}_{X}=K$.
Proof.
Under our assumptions
where $q(u)={K^{\prime }_{-}}(u)$, $u\in (0,\hspace{0.1667em}1)$, is increasing and left continuous. Let us define a probability space $(\varOmega ,\hspace{0.1667em}\mathcal{F},\mathsf{P})$ as follows: $\varOmega =(0,\hspace{0.1667em}1)$, $\mathcal{F}$ is the Borel σ-field and $\mathsf{P}$ is the Lebesgue measure. Put $X(\omega ):=q(\omega )$. Now if $G(x):=\inf \{u\in (0,\hspace{0.1667em}1):q(u)>x\}$, then it is easy to verify that $q(u)\le x\hspace{0.2778em}\Leftrightarrow \hspace{0.2778em}G(x)\ge u$, cf. (11). It follows that G is the distribution function of X and, hence, $q={q_{X}^{L}}$ on $(0,\hspace{0.1667em}1)$. This means that the left-hand derivative of K and $\mathsf{K}_{X}$ coincide on $(0,\hspace{0.1667em}1)$. In addition, their minimums over this interval are equal to zero. Therefore, $K=\mathsf{K}_{X}$ on (0, 1) and, hence, everywhere on $\mathbb{R}$. □
Remark 1.
An alternative way to prove Theorem 4 is to introduce the Fenchel transform J of K and to show that J satisfies the assumptions of Theorem 2. However, our proof yields not only a characterization statement of Theorem 4 but also an explicit representation of a random variable with a given integrated quantile function. Of course, this representation (namely, of a random variable with given distribution as its quantile function with respect to the Lebesgue measure on $(0,\hspace{0.1667em}1)$) is well known.
It is convenient to introduce shifted integrated quantile functions:
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle {\mathsf{K}_{X}^{[0]}}(u):=\mathsf{K}_{X}(u)-\mathsf{K}_{X}(0),\hspace{1em}u\in [0,\hspace{0.1667em}1],\hspace{2em}\text{if}\hspace{0.1667em}\hspace{2.5pt}\mathsf{K}_{X}(0)=\mathsf{E}\big[{X}^{-}\big]<\infty ,\\{} & \displaystyle {\mathsf{K}_{X}^{[1]}}(u):=\mathsf{K}_{X}(u)-\mathsf{K}_{X}(1),\hspace{1em}u\in [0,\hspace{0.1667em}1],\hspace{2em}\text{if}\hspace{0.1667em}\hspace{2.5pt}\mathsf{K}_{X}(1)=\mathsf{E}\big[{X}^{+}\big]<\infty .\end{array}\]
Now we can express the functions defined in (4)–(6) in terms of shifted integrated quantile functions. If $\mathsf{E}[{X}^{-}]<\infty $, then the absolute Lorenz curve coincides with ${\mathsf{K}_{X}^{[0]}}$:
Since $\varPsi _{X}$ is obtained from $\mathsf{J}_{X}$ by adding a constant $\mathsf{E}[{X}^{-}]=\mathsf{K}_{X}(0)$ by Corollary 1, the absolute Lorenz curve is the Fenchel transform of $\varPsi _{X}$:
\[ \operatorname{AL}_{X}(u)=\underset{x\in \mathbb{R}}{\sup }\big\{xu-\varPsi _{X}(x)\big\},\hspace{1em}u\in [0,\hspace{0.1667em}1].\]
The Conditional Value at Risk satisfies
The Hardy–Littlewood maximal function satisfies
2.3 Convex orders
Let us recall the definitions of convex orders in the univariate case.
For an arbitrary function $\psi :\mathbb{R}\to \mathbb{R}_{+}$, define $C_{\psi }$ as the space of all continuous functions $f:\mathbb{R}\to \mathbb{R}$ such that
Let X and Y be random variables. We say that
-
• X is less than Y in convex order ($X\le _{cx}Y$) if $\mathsf{E}|X|<\infty $, $\mathsf{E}|Y|<\infty $, and $\mathsf{E}[\varphi (X)]\le \mathsf{E}[\varphi (Y)]$ for any convex function $\varphi \in C_{|x|}$;
-
• X is less than Y in increasing convex order ($X\le _{icx}Y$) if $\mathsf{E}[{X}^{+}]<\infty $, $\mathsf{E}[{Y}^{+}]<\infty $, and $\mathsf{E}[\varphi (X)]\le \mathsf{E}[\varphi (Y)]$ for any increasing convex function $\varphi \in C_{{x}^{+}}$;
-
• X is less than Y in decreasing convex order ($X\le _{decx}Y$) if $\mathsf{E}[{X}^{-}]<\infty $, $\mathsf{E}[{Y}^{-}]<\infty $, and $\mathsf{E}[\varphi (X)]\le \mathsf{E}[\varphi (Y)]$ for any decreasing convex function $\varphi \in C_{{x}^{-}}$.
It is trivial that $X\le _{icx}Y$ if and only if $-X\le _{decx}-Y$. Also it is easy to see that $X\le _{cx}Y$ if and only if $X\le _{icx}Y$ and $X\le _{decx}Y$.
The following theorem is well known. We provide its proof which reduces to the duality between integrated distribution and quantile functions.
Theorem 5.
Let X and Y be random variables.
-
(i) If $\mathsf{E}|X|<\infty $, $\mathsf{E}|Y|<\infty $, then the following statements are equivalent:
-
(a) $X\le _{cx}Y$;
-
(b) ${\mathsf{K}_{X}^{[1]}}(u)\ge {\mathsf{K}_{Y}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$ and ${\mathsf{K}_{X}^{[1]}}(0)={\mathsf{K}_{Y}^{[1]}}(0)$;
-
(c) ${\mathsf{K}_{X}^{[0]}}(u)\ge {\mathsf{K}_{Y}^{[0]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$ and ${\mathsf{K}_{X}^{[0]}}(1)={\mathsf{K}_{Y}^{[0]}}(1)$;
-
(d) ${\mathsf{K}_{X}^{[1]}}(u)\ge {\mathsf{K}_{Y}^{[1]}}(u)$ and ${\mathsf{K}_{X}^{[0]}}(u)\ge {\mathsf{K}_{Y}^{[0]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$.
-
-
(ii) $X\le _{icx}Y$ if and only if $\mathsf{E}[{X}^{+}]<\infty $, $\mathsf{E}[{Y}^{+}]<\infty $, and ${\mathsf{K}_{X}^{[1]}}(u)\ge {\mathsf{K}_{Y}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$;
-
(iii) $X\le _{decx}Y$ if and only if $\mathsf{E}[{X}^{-}]<\infty $, $\mathsf{E}[{Y}^{-}]<\infty $, and ${\mathsf{K}_{X}^{[0]}}(u)\ge {\mathsf{K}_{Y}^{[0]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$.
Proof.
First, let us prove (ii). It is well known (see, e. g., [24]) that $X\le _{icx}Y$ if and only if $\mathsf{E}[{X}^{+}]<\infty $, $\mathsf{E}[{Y}^{+}]<\infty $, and $\mathsf{E}[{(X-x)}^{+}]\le \mathsf{E}[{(Y-x)}^{+}]$ for all $x\in \mathbb{R}$. Taking (8) into account, the last condition can be rewritten as
which in turn, is equivalent to
by the definition of integrated quantile function. The claim follows.
Now, (iii) follows from (ii) and the first part of the remark before Theorem 5. Now, the second part of this remark shows equivalence (a) ⇔ (d) in (i).
Next, the equalities in (b) and (c) are both equivalent to $\mathsf{E}[X]=\mathsf{E}[Y]$. On the other hand, the inequalities in (d) reduce to $-\mathsf{E}[X]\ge -\mathsf{E}[Y]$ and $\mathsf{E}[X]\ge \mathsf{E}[Y]$ for $u=0$ and $u=1$ respectively. It follows that (d) implies (b) and (c). Finally, it is straightforward to check that (b) and (c) are equivalent and, hence, imply (d). □
2.4 Examples
In this subsection we demonstrate how the developed techniques can be used to derive two elementary well-known inequalities, see [10, p. 152]. This approach allows us to find the distributions at which the corresponding extrema are attained. So the inequalities obtained in this way are sharp.
Example 1.
Let X be a random variable with zero mean and finite variance $\mathsf{D}(X)={\sigma }^{2}$. It is required to find a sharp upper bound for the probability $\mathsf{P}(X\ge t)$, where t is a fixed positive number.
We solve a converse problem. Namely, let $p:=\mathsf{P}(X\ge t)$ be fixed. Our purpose is to find a sharp lower bound for variances $\mathsf{D}(X)=\mathsf{E}[{X}^{2}]$ over all random variables X such that $\mathsf{E}[X]=0$, and $\mathsf{P}(X\ge t)=p$.
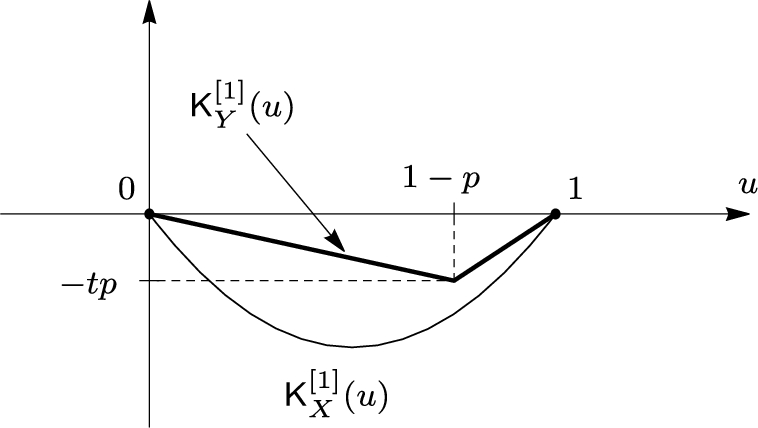
Fig. 3.
Graphs of shifted integrated quantile functions ${\mathsf{K}_{X}^{[1]}}$ and ${\mathsf{K}_{Y}^{[1]}}$ in Example 1
The above class of distributions has a minimal element with respect to the convex order. Indeed, let Y be a discrete random variable with $\mathsf{P}(Y=t)=p$ and $\mathsf{P}(Y=-\frac{tp}{1-p})=1-p$. It is clear that $\mathsf{E}[Y]=0$ and $\mathsf{P}(Y\ge t)=p$. If X is another random variable with these properties, then ${\mathsf{K}_{X}^{[1]}}(u)\le {\mathsf{K}_{Y}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$. Indeed, ${\mathsf{K}_{X}^{[1]}}(0)={\mathsf{K}_{Y}^{[1]}}(0)=0$ and the graph of ${\mathsf{K}_{Y}^{[1]}}$ consists of two straight segments, see Fig. 3. Since $\mathsf{P}(X\ge t)=p$, ${q_{X}^{R}}(u)\ge t$ for $u\in [1-p,\hspace{0.1667em}1]$. In particular,
\[ {\mathsf{K}_{X}^{[1]}}(1-p)=-{\int _{1-p}^{1}}{q_{X}^{R}}(s)\hspace{0.1667em}ds\le -pt={\mathsf{K}_{Y}^{[1]}}(1-p)\text{.}\]
Due to convexity of integrated quantile functions, this implies ${\mathsf{K}_{X}^{[1]}}(u)\le {\mathsf{K}_{Y}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$, see Fig. 3. Hence, $X\ge _{cx}Y$ by Theorem 5 (i). Therefore, $\mathsf{E}[f(X)]\ge \mathsf{E}[f(Y)]$ for any convex function f. In particular, ${\sigma }^{2}=\mathsf{E}[{X}^{2}]\ge \mathsf{E}[{Y}^{2}]=\frac{{t}^{2}p}{1-p}$. Resolving this inequality with respect to $p=\mathsf{P}(X\ge t)$, we obtain the required upper bound
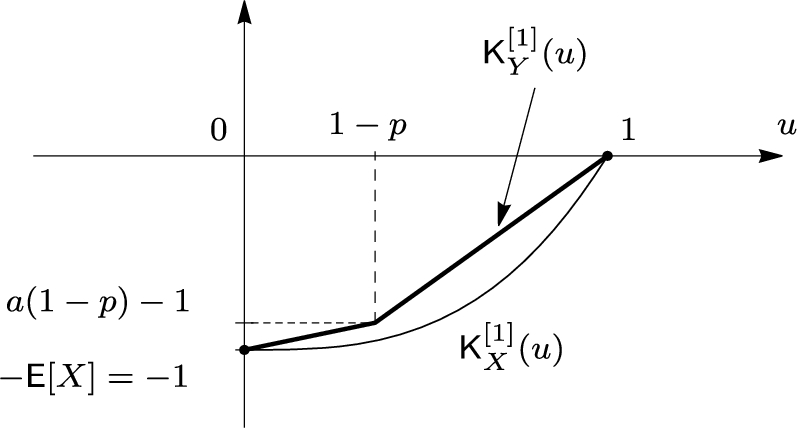
To show that the estimate in (18) is sharp it is enough to put $p=\frac{{\sigma }^{2}}{{\sigma }^{2}+{t}^{2}}$ in the definition of a random variable Y and to check that $\mathsf{E}[{Y}^{2}]={\sigma }^{2}$ and, for $X=Y$, the equality holds in (18).Example 2.
Let X be a strictly positive random variable, i.e. $F_{X}(0)=0$, such that $\mathsf{E}[X]=1$ and $\mathsf{E}[{X}^{2}]=b$. It is required to find a sharp lower bound for the probability $\mathsf{P}(X>a)$, where $a\in (0,\hspace{0.1667em}1)$ is fixed.
We will proceed in the similar way as in the previous example. Namely, let $p:=\mathsf{P}(X>a)$ be fixed. Our purpose is to find a sharp lower bound for the second moment $\mathsf{E}[{X}^{2}]$ over all random variables X such that $F_{X}(0)=0$, $\mathsf{E}[X]=1$ and $\mathsf{P}(X>a)=p$.
The above class of distributions has a minimal element with respect to the convex order. Indeed, let Y be a random variable such that $\mathsf{P}(Y=a)=1-p$ and $\mathsf{P}(Y=\frac{1-a(1-p)}{p})=p$. It is obvious that $F_{Y}(0)=0$, $\mathsf{E}[Y]=1$, and $\mathsf{P}(Y>a)=p$. If X is another random variable with these properties, then ${\mathsf{K}_{X}^{[1]}}(u)\le {\mathsf{K}_{Y}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$. Indeed, ${\mathsf{K}_{X}^{[1]}}(0)={\mathsf{K}_{Y}^{[1]}}(0)=-1$ and the graph of ${\mathsf{K}_{Y}^{[1]}}$ consists of two straight segments, see Fig. 4. Since $\mathsf{P}(X\le a)=1-p$, ${q_{X}^{L}}(u)\le a$ for $u\in [0,\hspace{0.1667em}1-p]$. In particular,
\[ {\mathsf{K}_{X}^{[1]}}(1-p)={\int _{0}^{1-p}}{q_{X}^{L}}(s)\hspace{0.1667em}ds-\mathsf{E}[X]\le a(1-p)-1={\mathsf{K}_{Y}^{[1]}}(1-p).\]
Due to convexity of integrated quantile functions, this implies ${\mathsf{K}_{X}^{[1]}}(u)\le {\mathsf{K}_{Y}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$, see Fig. 4. Hence, $X\ge _{cx}Y$ by Theorem 5 (i). Therefore, $\mathsf{E}[f(X)]\ge \mathsf{E}[f(Y)]$ for any convex function f. In particular, $b=\mathsf{E}[{X}^{2}]\ge \mathsf{E}[{Y}^{2}]={a}^{2}(1-p)+\frac{{(1-a(1-p))}^{2}}{{p}^{2}}p$. Resolving this inequality with respect to $p=\mathsf{P}(X>a)$, we obtain the required lower bound
The sharpness of the estimate in (19) follows if we put $p=\frac{{(1-a)}^{2}}{b-a(2-a)}$ in the definition of a random variable Y and verify that $\mathsf{E}[{Y}^{2}]=b$ and, for $X=Y$, the equality holds in (19). Remark that replacing the right-hand side in (19) by a smaller quantity $\frac{{(1-a)}^{2}}{b}$, we arrive at the inequality (7.6) in [10, p. 152].Fig. 4.
Graphs of shifted integrated quantile functions ${\mathsf{K}_{X}^{[1]}}$ and ${\mathsf{K}_{Y}^{[1]}}$ in Example 2
3 Uniform integrability and weak convergence
3.1 Tightness and uniform integrability
In this subsection we study conditions for tightness and uniform integrability of a family of random variables in terms of integrated quantile function. It is a natural question because both tightness and uniform integrability are characterized in terms of one-dimensional distributions of these variables.
Theorem 6.
Let $(X_{\alpha })$ be a family of random variables. Then the following statements are equivalent:
-
(i) The family of distributions $\{\operatorname{Law}(X_{\alpha })\}$ is tight.
-
(ii) For every $u,\hspace{0.1667em}v\in (0,\hspace{0.1667em}1)$, $\sup _{\alpha }|\mathsf{K}_{X_{\alpha }}(u)-\mathsf{K}_{X_{\alpha }}(v)|<\infty $.
-
(iii) The family of functions $\{\mathsf{K}_{X_{\alpha }}\}$ is pointwise bounded on $(0,\hspace{0.1667em}1)$.
-
(iv) The family of functions $\{\mathsf{K}_{X_{\alpha }}\}$ is equicontinuous on every $[a,\hspace{0.1667em}b]\subset (0,\hspace{0.1667em}1)$.
Proof.
(i) ⇒ (iv) Let $[a,\hspace{0.1667em}b]\subset (0,\hspace{0.1667em}1)$. The tightness condition implies that there is $C>0$ such that $F_{X_{\alpha }}(-C)<a$ and $F_{X_{\alpha }}(C)\ge b$ for all α. Hence, $-C<{q_{X_{\alpha }}^{L}}(u)\le C$ for all α and $u\in [a,\hspace{0.1667em}b]$. Thus, the functions $\mathsf{K}_{X_{\alpha }}$ are even uniformly Lipschitz continuous on $[a,\hspace{0.1667em}b]$.
(ii) ⇒ (iii) Let $c\in (0,\hspace{0.1667em}1)$. Take $a\in (0,\hspace{0.1667em}c)$ and $b\in (c,\hspace{0.1667em}1)$. By the assumption, there is $L>0$ such that $\mathsf{K}_{X_{\alpha }}(a)-\mathsf{K}_{X_{\alpha }}(c)\le L$ and $\mathsf{K}_{X_{\alpha }}(b)-\mathsf{K}_{X_{\alpha }}(c)\le L$ for all α. Let $u_{0,\alpha }$ be a point, where $\mathsf{K}_{X_{\alpha }}(u_{0,\alpha })=0$. If α is such that $u_{0,\alpha }<c$, then, by the three chord inequality,
\[ \frac{\mathsf{K}_{X_{\alpha }}(c)}{c-u_{0,\alpha }}\le \frac{\mathsf{K}_{X_{\alpha }}(b)-\mathsf{K}_{X_{\alpha }}(c)}{b-c}\text{,}\]
therefore, $\mathsf{K}_{X_{\alpha }}(c)\le cL/(b-c)$. Similarly, if α is such that $u_{0,\alpha }>c$, then $\mathsf{K}_{X_{\alpha }}(c)\le (1-c)L/(c-a)$.(ii) ⇒ (i) Let $\varepsilon >0$. By the assumption, there is $L>0$ such that $\mathsf{K}_{X_{\alpha }}(\varepsilon )-\mathsf{K}_{X_{\alpha }}(\varepsilon /2)>-L$ and $\mathsf{K}_{X_{\alpha }}(1-\varepsilon /2)-\mathsf{K}_{X_{\alpha }}(1-\varepsilon )\le L$ for all α. The first inequality yields
\[ -L<\mathsf{K}_{X_{\alpha }}(\varepsilon )-\mathsf{K}_{X_{\alpha }}(\varepsilon /2)={\int _{\varepsilon /2}^{\varepsilon }}{q_{X_{\alpha }}^{L}}(s)\hspace{0.1667em}ds\le \frac{\varepsilon }{2}{q_{X_{\alpha }}^{L}}(\varepsilon )\text{,}\]
which shows that $-\frac{2L}{\varepsilon }<{q_{X_{\alpha }}^{L}}(\varepsilon )$ and, hence, $F_{X_{\alpha }}(-\frac{2L}{\varepsilon })<\varepsilon $. Similarly, from the second inequality, one gets $F_{X_{\alpha }}(\frac{2L}{\varepsilon })\ge 1-\varepsilon $ for all α. This proves the tightness of the laws of $X_{\alpha }$.Since implications (iv) ⇒ (ii) and (iii) ⇒ (ii) are obvious, the claim follows. □
Theorem 7.
Let $\{X_{\alpha }\}$ be a family of random variables. Then the following statements are equivalent:
-
(i) The family $\{X_{\alpha }\}$ is uniformly integrable.
-
(ii) The family of integrated quantile functions $\{\mathsf{K}_{X_{\alpha }}\}$ is equicontinuous on $[0,\hspace{0.1667em}1]$.
-
(iii) The family of integrated quantile functions $\{\mathsf{K}_{X_{\alpha }}\}$ is relatively compact in the space $C[0,\hspace{0.1667em}1]$ of continuous functions with supremum norm.
Proof.
Let us consider the probability space $(\varOmega ,\hspace{0.1667em}\mathcal{F},\hspace{0.1667em}\mathsf{P})$ as in the proof of Theorem 4 and define random variables $Y_{\alpha }(\omega )={q_{X_{\alpha }}^{L}}(\omega )$. Then $X_{\alpha }\stackrel{d}{=}Y_{\alpha }$ and it is enough to study the uniform integrability of the family $\{Y_{\alpha }\}$. Without loss of generality, we suppose that $X_{\alpha }=Y_{\alpha }$.
Let us recall that a family $\{X_{\alpha }\}$ is uniformly integrable if and only if $\mathsf{E}|X_{\alpha }|$ are bounded and $\mathsf{E}[|X_{\alpha }|\mathbb{1}_{A}]$ are uniformly continuous, i. e. $\sup _{\alpha }\mathsf{E}[|X_{\alpha }|\mathbb{1}_{A}]\to 0$ as $\mathsf{P}(A)\to 0$; moreover, the boundedness of $\mathsf{E}|X_{\alpha }|$ is a consequence of the uniform continuity if the measure $\mathsf{P}$ has no atomic part, in particular, in our case. On the other hand, by the Arzela–Ascoli theorem a set in $C[0,\hspace{0.1667em}1]$ is relatively compact if and only if it is uniformly bounded and equicontinuous.
We shall check that the uniform boundedness and the equicontinuity of $\{\mathsf{K}_{X_{\alpha }}\}$ are equivalent to uniform boundedness of $\mathsf{E}|X_{\alpha }|$ and the uniform continuity of $\mathsf{E}[|X_{\alpha }|\mathbb{1}_{A}]$, respectively. In view of the above this is sufficient for the proof of the theorem.
By the properties of integrated quantile functions,
\[ \underset{u\in [0,\hspace{0.1667em}1]}{\sup }\mathsf{K}_{X_{\alpha }}(u)=\max \big(\mathsf{E}\big[{X_{\alpha }^{-}}\big],\hspace{0.1667em}\mathsf{E}\big[{X_{\alpha }^{+}}\big]\big)\le \mathsf{E}|X_{\alpha }|\le 2\underset{u\in [0,\hspace{0.1667em}1]}{\sup }\mathsf{K}_{X_{\alpha }}(u)\text{.}\]
Hence, $\sup _{\alpha }\mathsf{E}|X_{\alpha }|<\infty $ if and only if the family $\{\mathsf{K}_{X_{\alpha }}\}$ is uniformly bounded.For a fixed $\varepsilon >0$, let $\delta >0$ be such that $\sup _{\alpha }\mathsf{E}[|X_{\alpha }|\mathbb{1}_{A}]<\varepsilon $ for any Borel set $A\subseteq (0,\hspace{0.1667em}1)$ with $\mathsf{P}(A)<\delta $. Let $u_{1},u_{2}\in [0,\hspace{0.1667em}1]$ satisfy $0<u_{2}-u_{1}<\delta $. Then, for any α,
Conversely, fix $\varepsilon >0$ and let $\delta >0$ be such that $|\mathsf{K}_{X_{\alpha }}(u_{2})-\mathsf{K}_{X_{\alpha }}(u_{1})|<\varepsilon $ for all α if $|u_{2}-u_{1}|<\delta $. Since $X_{\alpha }(\omega )$ is increasing in ω, the following inequality holds for any Borel subset $A\subseteq (0,\hspace{0.1667em}1)$:
Therefore, if $\mathsf{P}(A)<\delta $ then
(20)
\[ \int _{(0,\hspace{0.1667em}\mathsf{P}(A)]}X_{\alpha }(\omega )\hspace{0.1667em}d\omega \le \int _{A}X_{\alpha }(\omega )\hspace{0.1667em}d\omega \le \int _{[1-\mathsf{P}(A),\hspace{0.1667em}1)}X_{\alpha }(\omega )\hspace{0.1667em}d\omega \text{.}\]
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathsf{E}\big[|X_{\alpha }|\mathbb{1}_{A}\big]& \displaystyle =\int _{A\cap \{X_{\alpha }<0\}}-X_{\alpha }(\omega )\hspace{0.1667em}d\omega +\int _{A\cap \{X_{\alpha }>0\}}X_{\alpha }(\omega )\hspace{0.1667em}d\omega \\{} & \displaystyle \le \int _{(0,\hspace{0.1667em}\mathsf{P}(A\cap \{X_{\alpha }<0\})]}-X_{\alpha }(\omega )\hspace{0.1667em}d\omega +\int _{[1-\mathsf{P}(A\cap \{X_{\alpha }>0\}),\hspace{0.1667em}1)}X_{\alpha }(\omega )\hspace{0.1667em}d\omega \\{} & \displaystyle \le \underset{u\in (0,\mathsf{P}(A)]}{\max }\big(\mathsf{K}_{X_{\alpha }}(0)-\mathsf{K}_{X_{\alpha }}(u)\big)+\underset{u\in [1-\mathsf{P}(A),1)}{\max }\big(\mathsf{K}_{X_{\alpha }}(1)-\mathsf{K}_{X_{\alpha }}(u)\big)\\{} & \displaystyle <2\varepsilon \text{.}\end{array}\]
□The following criterion of uniform integrability is proved in [17].
Theorem 8 (Leskelä and Vihola).
A family $\{X_{\alpha }\}$ of integrable random variables is uniformly integrable if and only if there is an integrable random variable X such that $|X_{\alpha }|\le _{icx}X$ for all α.
Proof.
Without loss of generality, we may assume that all $X_{\alpha }$ are nonnegative. To simplify notation, let $K_{\alpha }(u):={\mathsf{K}_{X_{\alpha }}^{[1]}}(u)$, $u\in [0,\hspace{0.1667em}1]$. Then $K_{\alpha }$ are increasing continuous convex functions with $K_{\alpha }(1)=0$. According to Theorems 4, 5 (ii) and 7, it is enough to prove that the family $\{K_{\alpha }\}$ is equicontinuous if and only if there is an increasing continuous convex function $K(u)$, $u\in [0,\hspace{0.1667em}1]$, with $K(1)=0$ such that
The sufficiency is evident. Indeed, if $0\le u_{1}\le u_{2}\le 1$, then, for all α,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle 0\le K_{\alpha }(u_{2})-K_{\alpha }(u_{1})& \displaystyle \le K_{\alpha }(1)-K_{\alpha }\big(1-(u_{2}-u_{1})\big)=-K_{\alpha }\big(1-(u_{2}-u_{1})\big)\\{} & \displaystyle \le -K\big(1-(u_{2}-u_{1})\big)=K(1)-K\big(1-(u_{2}-u_{1})\big)\text{,}\end{array}\]
and the equicontinuity follows from the continuity of K.Let us define K as the lower semicontinuous convex envelope of $\inf _{\alpha }K_{\alpha }$. To prove the necessity, it is enough to show that $K(1)=0$ if the family $\{K_{\alpha }\}$ is equicontinuous. Fix $\varepsilon >0$ and let $\delta >0$ be such that $|K_{\alpha }(u_{2})-K_{\alpha }(u_{1})|<\varepsilon $ for all α if $|u_{2}-u_{1}|\le \delta $. In particular, $K_{\alpha }(1-\delta )>-\varepsilon $. Since $K_{\alpha }$ is convex, we have $K_{\alpha }(u)>-\frac{\varepsilon }{\delta }(1-u)$ for all $u\in [0,\hspace{0.2778em}1-\delta ]$ and for all α. Moreover, since $K_{\alpha }$ is increasing, $K_{\alpha }(u)\ge -\varepsilon $ for all $u\in [1-\delta ,\hspace{0.2778em}1]$ and for all α. Combining, we get
\[ \underset{\alpha }{\inf }K_{\alpha }(u)\ge \min \bigg(-\frac{\varepsilon }{\delta }(1-u),-\varepsilon \bigg)\ge -\frac{\varepsilon }{\delta }+\frac{\varepsilon (1-\delta )}{\delta }u\text{,}\]
for all $u\in [0,\hspace{0.1667em}1]$. It follows that $K(u)\ge -\frac{\varepsilon }{\delta }+\frac{\varepsilon (1-\delta )}{\delta }u$ for all $u\in [0,\hspace{0.1667em}1]$, in particular, $K(1-\delta )>-2\varepsilon $. The claim follows. □3.2 Weak convergence
In this subsection $(X_{n})$ is a sequence of random variables.
Theorem 9.
The following statements are equivalent:
-
(i) The sequence $(X_{n})$ weakly converges.
-
(ii) There is a sequence $(c_{n})$ of numbers such that, for every $u\in (0,\hspace{0.1667em}1)$, the sequence $(\mathsf{K}_{X_{n}}(u)-c_{n})$ converges to a finite limit.
-
(iii) The sequence $(\mathsf{K}_{X_{n}})$ converges uniformly on every $[\alpha ,\hspace{0.1667em}\beta ]\subseteq (0,\hspace{0.1667em}1)$.
Moreover, in this case if X is a weak limit of $(X_{n})$, then $\mathsf{K}_{X}(u)=\lim _{n\to \infty }\mathsf{K}_{X_{n}}(u)$ for all $u\in (0,\hspace{0.1667em}1)$.
Remark 2.
If $\mathsf{E}[{X_{n}^{-}}]<\infty $ (resp. $\mathsf{E}[{X_{n}^{+}}]<\infty $) for all n, then the pointwise convergence of ${\mathsf{K}_{X_{n}}^{[0]}}$ (resp. ${\mathsf{K}_{X_{n}}^{[1]}}$) on $(0,\hspace{0.1667em}1)$ is sufficient (use Theorem 9, $(\mathrm{ii})$ ⇒ $(\mathrm{i})$) but not necessary for the weak convergence of $X_{n}$.
Theorem 10.
Let $(X_{n})$ weakly converge and $\mathsf{E}|X_{n}|<\infty $ (resp. $\mathsf{E}[{X_{n}^{-}}]<\infty $, resp. $\mathsf{E}[{X_{n}^{+}}]<\infty $). Then the following statements are equivalent:
-
(i) The sequence $(|X_{n}|)$ (resp. $({X_{n}^{-}})$, resp. $({X_{n}^{+}})$) is uniformly integrable.
-
(ii) The sequence of functions $(\mathsf{K}_{X_{n}})$ converges pointwise on $[0,\hspace{0.1667em}1]$ (resp. $[0,\hspace{0.1667em}1)$, resp. $(0,\hspace{0.1667em}1]$) to a continuous function with finite values.
-
(iii) The sequence $(\mathsf{K}_{X_{n}})$ converges uniformly to a finite-valued function on $[0,\hspace{0.1667em}1]$ (resp. on every $[0,\hspace{0.1667em}\beta ]\subseteq [0,\hspace{0.1667em}1)$, resp. on every $[\alpha ,\hspace{0.1667em}1]\subseteq (0,\hspace{0.1667em}1]$).
Remark 3.
In contrast to Remark 2, a combination of the weak convergence of $X_{n}$ and the uniform integrability of ${X_{n}^{-}}$ (resp. ${X_{n}^{+}}$) can be expressed in terms of the shifted integrated quantile functions ${\mathsf{K}_{X_{n}}^{[0]}}$ (resp. ${\mathsf{K}_{X_{n}}^{[1]}}$). For instance, let a sequence $(X_{n})$ weakly converge to X and the sequence $({X_{n}^{+}})$ is uniformly integrable. Then the pointwise limit of ${\mathsf{K}_{X_{n}}^{[1]}}(u)$ satisfies
and is continuous on $(0,\hspace{0.1667em}1]$. Conversely, if the functions ${\mathsf{K}_{X_{n}}^{[1]}}$ converge pointwise to a continuous limit on $(0,\hspace{0.1667em}1]$, then $X_{n}$ weakly converges, say, to X (use Theorem 9, $(\mathrm{ii})$ ⇒ $(\mathrm{i})$). In particular, for any $u\in (0,\hspace{0.1667em}1)$,
(21)
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \underset{n\to \infty }{\lim }{\mathsf{K}_{X_{n}}^{[1]}}(u)& \displaystyle =\underset{n\to \infty }{\lim }\mathsf{K}_{X_{n}}(u)-\underset{n\to \infty }{\lim }\mathsf{E}\big[{X_{n}^{+}}\big]\\{} & \displaystyle =\mathsf{K}_{X}(u)-\mathsf{E}\big[{X}^{+}\big]={\mathsf{K}_{X}^{[1]}}(u),\hspace{1em}u\in (0,\hspace{0.1667em}1],\end{array}\]
\[ \underset{n\to \infty }{\lim }{\mathsf{K}_{X_{n}}^{[1]}}(u)=\underset{n\to \infty }{\lim }\mathsf{K}_{X_{n}}(u)-\underset{n\to \infty }{\lim }\mathsf{E}\big[{X_{n}^{+}}\big]=\mathsf{K}_{X}(u)-\underset{n\to \infty }{\lim }\mathsf{E}\big[{X_{n}^{+}}\big]\text{.}\]
Continuity of the limiting function in the left-hand side of the above formula at $u=1$ implies $\lim _{n\to \infty }\mathsf{E}[{X_{n}^{+}}]=\lim _{u\uparrow 1}\mathsf{K}_{X}(u)=\mathsf{E}[{X}^{+}]$.Proof of Theorems 9 and 10.
First, let us suppose that $(X_{n})$ weakly converges to X. It is well known that then ${q_{X_{n}}^{L}}(u)\to {q_{X}^{L}}(u)$ as $n\to \infty $ for every continuity point u of ${q_{X}^{L}}$. Put $u_{n,0}:=F_{X_{n}}(0)$ and $u_{0}:=F_{X}(0)$.
Assume for the moment that $X_{n}$ are uniformly bounded. Then, for any $u\in [0,\hspace{0.1667em}1]$,
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathsf{K}_{X_{n}}(u)& \displaystyle ={\int _{0}^{u}}q_{X_{n}}(s)\hspace{0.1667em}ds-{\int _{0}^{u_{n,0}}}q_{X_{n}}(s)\hspace{0.1667em}ds={\int _{0}^{u}}q_{X_{n}}(s)\hspace{0.1667em}ds+{\int _{0}^{1}}{\big(q_{X_{n}}(s)\big)}^{-}\hspace{0.1667em}ds\\{} & \displaystyle \to {\int _{0}^{u}}q_{X}(s)\hspace{0.1667em}ds+{\int _{0}^{1}}{\big(q_{X}(s)\big)}^{-}\hspace{0.1667em}ds=\mathsf{K}_{X}(u)\end{array}\]
by the dominated convergence theorem. Moreover, by Theorem 7 the sequence $(\mathsf{K}_{X_{n}})$ is relatively compact in $C[0,\hspace{0.1667em}1]$. Combined with pointwise convergence, this shows that $(\mathsf{K}_{X_{n}})$ converges to $\mathsf{K}_{X}$ uniformly on $[0,\hspace{0.1667em}1]$.If no assumptions on $X_{n}$ are imposed, let us introduce the function $g_{C}(x):=\max (\min (x,\hspace{0.1667em}C),\hspace{0.1667em}-C)$, $C>0$, and define random variables
Then $(Y_{n})$ weakly converges to Y. Hence, $\mathsf{K}_{Y_{n}}\to \mathsf{K}_{Y}$ uniformly on $[0,\hspace{0.1667em}1]$ as it has just been proved. However, $\mathsf{K}_{Y_{n}}=\mathsf{K}_{X_{n}}$ on $[F_{X_{n}}(-C),\hspace{0.1667em}F_{X_{n}}(C)]\ni u_{n,0}$ and $\mathsf{K}_{Y}=\mathsf{K}_{X}$ on $[F_{X}(-C),\hspace{0.1667em}F_{X}(C)]\ni u_{0}$. Given $[\alpha ,\hspace{0.1667em}\beta ]\subseteq (0,\hspace{0.1667em}1)$, choose $C>0$ so that $[\alpha ,\hspace{0.1667em}\beta ]\subseteq [F_{X}(-C),\hspace{0.1667em}F_{X}(C)]$ and $[\alpha ,\hspace{0.1667em}\beta ]\subseteq [F_{X_{n}}(-C),\hspace{0.1667em}F_{X_{n}}(C)]$ for all n, which is possible by tightness. Therefore, $\mathsf{K}_{X_{n}}(u)\to \mathsf{K}_{X}(u)$ uniformly in u on $[\alpha ,\hspace{0.1667em}\beta ]\subseteq (0,\hspace{0.1667em}1)$. In particular, $(\mathsf{K}_{X_{n}})$ converges pointwise to $\mathsf{K}_{X}$ on $(0,\hspace{0.1667em}1)$.
To complete the proof of Theorem 9 it remains to prove implication (ii) ⇒ (i). Let $u,v\in (0,\hspace{0.1667em}1)$. By the assumption, the sequence $\mathsf{K}_{X_{n}}(u)-\mathsf{K}_{X_{n}}(v)$ converges to a finite limit and, hence, is bounded. By Theorem 6, the laws of $X_{n}$ are tight. Let $(X_{n_{k}})$ be a weakly convergent subsequence. It follows from what has been proved that the integrated quantile function $K(u)$ of its limit coincides with $\lim _{k\to \infty }\mathsf{K}_{X_{n_{k}}}(u)$ for $u\in (0,\hspace{0.1667em}1)$. Therefore, for all $u\in (0,\hspace{0.1667em}1)$,
\[ \underset{n\to \infty }{\lim }\big(\mathsf{K}_{X_{n}}(u)-c_{n}\big)=\underset{k\to \infty }{\lim }\big(\mathsf{K}_{X_{n_{k}}}(u)-c_{n_{k}}\big)=K(u)-\underset{k\to \infty }{\lim }c_{n_{k}}\text{.}\]
This implies that $c_{n_{k}}$ converges to a finite limit and that $K(u)$ is obtained from $\lim _{n\to \infty }(\mathsf{K}_{X_{n}}(u)-c_{n})$ by adding a constant. Since K is an integrated quantile function, this constant is determined uniquely. Thus, K is the same for all weakly convergent subsequences, which means that $(X_{n})$ weakly converges.It is enough to prove Theorem 10 in one of three cases, for example, in the case $\mathsf{E}[{X_{n}^{-}}]<\infty $. Assume that $({X_{n}^{-}})$ is uniformly integrable. Then $\mathsf{E}[{X_{n}^{-}}]\to \mathsf{E}[{X}^{-}]$, where X is a weak limit of $(X_{n})$. In other words, $\mathsf{K}_{X_{n}}(0)\to \mathsf{K}_{X}(0)$. Thus, we have (ii). Moreover, the sequence $(\mathsf{K}_{{X_{n}^{-}}})$ is equicontinuous. It follows that $(\mathsf{K}_{X_{n}})$ converges uniformly on every segment $[0,\hspace{0.1667em}\beta ]\subseteq (0,\hspace{0.1667em}1)$. Implication (iii) ⇒ (ii) is trivial. If (ii) holds, then $\lim _{n\to \infty }\mathsf{K}_{X_{n}}(u)$ is a continuous function in $u\in [0,\hspace{0.1667em}1)$. On the other hand, this limit is $\mathsf{K}_{X}(u)$ for $u\in (0,\hspace{0.1667em}1)$. Hence, $\mathsf{E}[{X}^{-}]=\mathsf{K}_{X}(0)=\lim _{n\to \infty }\mathsf{E}[{X_{n}^{-}}]$, and the sequence $({X_{n}^{-}})$ is uniformly integrable. □
4 Applications to binary statistical models
The theory of statistical experiments deals with the problem of comparing the information in different experiments. The foundation of the theory of experiments was laid by Blackwell [1, 2], who first studied a notion of being more informative for experiments. Since it is difficult to give an explicit definition of statistical information, the theory of statistical experiments evaluates the performance of an experiment in terms of the set of available risk functions, in general, for arbitrary decision spaces and loss functions. For the theory of statistical experiments we refer to [15, 25], and especially to [27, 28], where the reader can find unexplained results and additional information.
In this paper we consider only binary statistical experiments, or dichotomies, $\mathbb{E}=(\varOmega ,\mathcal{F},\mathsf{P},{\mathsf{P}^{\prime }})$. It is known that for binary models, it is enough to deal with testing problems, i. e. with tests as decision rules and with the probabilities of errors of the first and the second kinds of a test.
Let us introduce some notation. $\mathsf{Q}$ is any probability measure dominating $\mathsf{P}$ and ${\mathsf{P}^{\prime }}$, $z:=d\mathsf{P}/d\mathsf{Q}$ and ${z^{\prime }}:=d{\mathsf{P}^{\prime }}/d\mathsf{Q}$ are the corresponding Radon–Nikodým derivatives. $\mathsf{E}$, ${\mathsf{E}^{\prime }}$, and $\mathsf{E}_{\mathsf{Q}}$ are the expectations with respect to $\mathsf{P}$, ${\mathsf{P}^{\prime }}$ and $\mathsf{Q}$ respectively. Note that $\mathsf{P}(z=0)=0$ and $Z:={z^{\prime }}/z$, where $0/0=0$ by convention, is the Radon–Nikodým derivative of the $\mathsf{P}$-absolutely continuous part of ${\mathsf{P}^{\prime }}$ with respect to $\mathsf{P}$.
For an experiment $\mathbb{E}=(\varOmega ,\mathcal{F},\mathsf{P},{\mathsf{P}^{\prime }})$, denote by $\varPhi (\mathbb{E})$ the set of all test functions φ in $\mathbb{E}$, i.e. measurable mappings from $(\varOmega ,\mathcal{F})$ to $[0,1]$. It is convenient for us to interpret $\varphi (\omega )$ as the probability to accept the null hypothesis $\mathsf{P}$ and to reject the alternative ${\mathsf{P}^{\prime }}$ if ω is observed. Then $\alpha (\varphi ):=\mathsf{E}[1-\varphi ]$ and $\beta (\varphi ):={\mathsf{E}^{\prime }}[\varphi ]$ are the probabilities of errors of the first and the second kind respectively of a test φ.
Denote
that is the smallest probability of the second kind error if the probability of the first kind error is u. It follows that the set $\mathfrak{N}(\mathbb{E})$ and the risk function $\mathsf{r}_{\mathbb{E}}$ are connected by
and
In particular, $\mathsf{r}_{\mathbb{E}}$ is a continuous convex decreasing function taking values in $[0,\hspace{0.1667em}1]$ and $\mathsf{r}_{\mathbb{E}}(1)=0$. Therefore, by Theorem 4, $\mathsf{r}_{\mathbb{E}}(u)$ coincides on $[0,\hspace{0.1667em}1]$ with an integrated quantile function corresponding to some distribution. The following result determines this distribution and explains why it is natural to use integrated quantile functions for binary models.
\[ \mathfrak{N}(\mathbb{E}):=\big\{\big(\mathsf{E}[\varphi ],\hspace{0.1667em}{\mathsf{E}^{\prime }}[\varphi ]\big):\varphi \in \varPhi (\mathbb{E})\big\}=\big\{\big(1-\alpha (\varphi ),\hspace{0.1667em}\beta (\varphi )\big):\varphi \in \varPhi (\mathbb{E})\big\}.\]
It is well known that $\mathfrak{N}(\mathbb{E})$ is a convex and closed subset of $[0,1]\times [0,1]$, contains $(0,0)$, and is symmetric with respect to the point $(1/2,1/2)$, see, e.g., [16, p. 62]. In Fig. 5 we present a set $\mathfrak{N}(\mathbb{E})$ of generic form. Introduce also the risk function
(22)
\[ \mathsf{r}_{\mathbb{E}}(u):=\inf \hspace{0.1667em}\big\{\beta (\varphi ):\varphi \in \varPhi (\mathbb{E}),\hspace{2.5pt}\alpha (\varphi )=u\big\},\hspace{1em}u\in [0,\hspace{0.1667em}1],\](23)
\[ \mathsf{r}_{\mathbb{E}}(u)=\inf \hspace{0.1667em}\big\{v:(1-u,v)\in \mathfrak{N}(\mathbb{E})\big\}\](24)
\[ \mathfrak{N}(\mathbb{E})=\big\{(u,\hspace{0.1667em}v)\in [0,\hspace{0.1667em}1]\times [0,\hspace{0.1667em}1]:\mathsf{r}_{\mathbb{E}}(1-u)\le v\le 1-\mathsf{r}_{\mathbb{E}}(u)\big\}\text{.}\]Fig. 5.
The shaded area represents the set $\mathfrak{N}(\mathbb{E})$. The thick curve corresponds to admissible, or Neyman–Pearson tests ${\varphi }^{\ast }$ with the following property: if $\alpha (\varphi )\le \alpha ({\varphi }^{\ast })$ and $\beta (\varphi )\le \beta ({\varphi }^{\ast })$ for some $\varphi \in \varPhi (\mathbb{E})$, then both inequalities are equalities. See [27, Chapter 2] for more details. The thick curve together with the horizontal segment $[0,\hspace{0.1667em}\mathsf{P}(Z>0)]\times \{0\}$ is the graph of the function $\mathsf{r}_{\mathbb{E}}(1-u)$
Proposition 1.
For all $u\in [0,\hspace{0.1667em}1]$, $\mathsf{r}_{\mathbb{E}}(u)=\mathsf{K}_{-Z}(u)$, where $\mathsf{K}_{-Z}$ is the integrated quantile function corresponding to the distribution of the negative likelihood ratio $-Z=-{z^{\prime }}/z$ under the null hypothesis.
Proof.
Let $\varphi _{0}\in \varPhi (\mathbb{E})$ and $x\in \mathbb{R}_{+}$. Then the straight line with the slope x and passing through the point $(\mathsf{E}[\varphi _{0}],\hspace{0.1667em}{\mathsf{E}^{\prime }}[\varphi _{0}])$ lies below the graph of $K(u):=\mathsf{r}_{\mathbb{E}}(1-u)$ on $[0,\hspace{0.1667em}1]$ if and only if, for every $\varphi \in \varPhi (\mathbb{E})$,
\[ {\mathsf{E}^{\prime }}[\varphi ]\ge {\mathsf{E}^{\prime }}[\varphi _{0}]+x\big(\mathsf{E}[\varphi ]-\mathsf{E}[\varphi _{0}]\big).\]
Passing to a dominating measure $\mathsf{Q}$, the above inequality can be rewritten as
This holds for every $\varphi \in \varPhi (\mathbb{E})$ if and only if
Let $u\in (0,\hspace{0.1667em}1)$ and take any $x\in [{q_{Z}^{L}}(u),{q_{Z}^{R}}(u)]$. Then $u\in [F_{Z}(x-0),F_{Z}(x)]$, so there is $\gamma \in [0,\hspace{0.1667em}1]$ such that $u=(1-\gamma )F_{Z}(x-0)+\gamma F_{Z}(x)$. Finally, put $\varphi _{0}:=\mathbb{1}_{\{{z^{\prime }}<xz\}}+\gamma \mathbb{1}_{\{{z^{\prime }}=xz\}}$. Since $Z={z^{\prime }}/z$ $\mathsf{P}$-a.s., we get $\mathsf{E}[\varphi _{0}]=u$ and, obviously, $\varphi _{0}$ satisfies (25). This means that $x\in \partial K(u)$. Conversely, let $u\in (0,\hspace{0.1667em}1)$ and $x\in \partial K(u)$. Take any $\varphi _{0}\in \varPhi (\mathbb{E})$ such that $\mathsf{E}[\varphi _{0}]=u$ and $\beta (\varphi _{0})=K(u)$. Then $\varphi _{0}$ satisfies (25), which implies $\mathsf{E}[\varphi _{0}]\in [F_{Z}(x-0),F_{Z}(x)]$. Hence, $x\in [{q_{Z}^{L}}(u),{q_{Z}^{R}}(u)]$.
It is clear that $K(0)=\mathsf{K}_{Z}(0)=0$. Now taking into account that K and $\mathsf{K}_{Z}$ are convex functions, $\mathsf{K}_{Z}$ is continuous on $[0,\hspace{0.1667em}1]$, and $\partial K(u)=\partial \mathsf{K}_{Z}(u)$ for $u\in (0,\hspace{0.1667em}1)$, it remains to prove that $K(1)\le \mathsf{K}_{Z}(1)=\mathsf{E}[Z]$. This is easy: take $\varphi _{0}:=\mathbb{1}_{\{z>0\}}$, then $\mathsf{E}[\varphi _{0}]=1$ and ${\mathsf{E}^{\prime }}[\varphi _{0}]={\mathsf{P}^{\prime }}(z>0)=\mathsf{E}_{\mathsf{Q}}[{z^{\prime }}\mathbb{1}_{\{z>0\}}]=\mathsf{E}[Z]$. Finally, $\mathsf{r}_{\mathbb{E}}(u)=K(1-u)=\mathsf{K}_{Z}(1-u)=\mathsf{K}_{-Z}(u)$. □
Remark 4.
A usual way to prove that the set $\mathfrak{N}(\mathbb{E})$ is closed is based on weak compactness of test functions, see, e.g., [16]. The reader may readily verify that the closedness of $\mathfrak{N}(\mathbb{E})$ follows directly from the above proof.
Let us also introduce the minimum Bayes risk function (the error function)
In particular, it follows from Theorem 1 that
\[ \mathsf{b}_{\mathbb{E}}(\pi ):=\underset{\varphi \in \varPhi (\mathbb{E})}{\inf }\big((1-\pi )\alpha (\varphi )+\pi \beta (\varphi )\big),\hspace{1em}\pi \in [0,\hspace{0.1667em}1].\]
It can be expressed in terms of risk function $\mathsf{r}_{\mathbb{E}}$ and vice versa. Indeed, for any $\pi \in (0,\hspace{0.1667em}1)$,
(26)
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathsf{b}_{\mathbb{E}}(\pi )& \displaystyle =\underset{u\in [0,\hspace{0.1667em}1]}{\inf }\big((1-\pi )u+\pi \mathsf{r}_{\mathbb{E}}(u)\big)\\{} & \displaystyle =-\pi \underset{u\in [0,\hspace{0.1667em}1]}{\sup }\bigg(-\frac{1-\pi }{\pi }u-\mathsf{r}_{\mathbb{E}}(u)\bigg)=-\pi \underset{u\in [0,\hspace{0.1667em}1]}{\sup }\bigg(-\frac{1-\pi }{\pi }u-\mathsf{K}_{-Z}(u)\bigg)=\\{} & \displaystyle =-\pi \mathsf{J}_{-Z}\bigg(-\frac{1-\pi }{\pi }\bigg)=1-\pi -\pi \mathsf{J}_{Z}\bigg(\frac{1-\pi }{\pi }\bigg)\text{.}\end{array}\]
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \underset{\pi \downarrow 0}{\lim }\frac{\mathsf{b}_{\mathbb{E}}(\pi )}{\pi }& \displaystyle =\underset{x\to +\infty }{\lim }\big(x-\mathsf{J}_{Z}(x)\big)=\mathsf{E}[Z],\\{} \displaystyle \underset{\pi \uparrow 1}{\lim }\frac{\mathsf{b}_{\mathbb{E}}(\pi )}{1-\pi }& \displaystyle =1-\underset{x\downarrow 0}{\lim }\frac{\mathsf{J}_{Z}(x)}{x}=\mathsf{P}(Z>0),\end{array}\]
see [27, Lemma 14.6] and [28, p. 607].Conversely, using Definition 2 and (26), we get, for $u\in [0,\hspace{0.1667em}1]$,
see [28, p. 590]. Here we have used that $\mathsf{J}_{-Z}(x)=x$ for $x\ge 0$.
(27)
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathsf{r}_{\mathbb{E}}(u)& \displaystyle =\mathsf{K}_{-Z}(u)=\underset{x\in \mathbb{R}}{\sup }\big(xu-\mathsf{J}_{-Z}(x)\big)=\underset{x<0}{\sup }\big(xu-\mathsf{J}_{-Z}(x)\big)\\{} & \displaystyle =\underset{\pi \in (0,\hspace{0.1667em}1)}{\sup }\bigg(-\frac{1-\pi }{\pi }u-\mathsf{J}_{-Z}\bigg(-\frac{1-\pi }{\pi }\bigg)\bigg)=\underset{\pi \in (0,\hspace{0.1667em}1)}{\sup }\frac{1}{\pi }\big(\mathsf{b}_{\mathbb{E}}(\pi )-(1-\pi )u\big),\end{array}\]Finally, let us introduce one more characteristic of binary models, namely the distribution of the ‘likelihood ratio’
Now let us present some basic notions and results from the theory of comparison of dichotomies. All these facts are well known, see e. g. [27, Chapter 3] and [28, Chapter 10]. Our aim is to show how they can be deduced with the help of the results in Sections 2 and 3.
Definition 3.
Let $\mathbb{E}=(\varOmega ,\mathcal{F},\mathsf{P},{\mathsf{P}^{\prime }})$ and $\widetilde{\mathbb{E}}=(\widetilde{\varOmega },\widetilde{\mathcal{F}},\widetilde{\mathsf{P}},{\widetilde{\mathsf{P}}^{\prime }})$ be two binary experiments. $\mathbb{E}$ is said to be more informative than $\widetilde{\mathbb{E}}$, denoted by $\mathbb{E}\succeq \widetilde{\mathbb{E}}$ or $\widetilde{\mathbb{E}}\preceq \mathbb{E}$, if $\mathfrak{N}(\mathbb{E})\supseteq \mathfrak{N}(\widetilde{\mathbb{E}})$. $\mathbb{E}$ and $\widetilde{\mathbb{E}}$ are called equivalent ($\mathbb{E}\sim \widetilde{\mathbb{E}}$) if $\mathbb{E}\succeq \widetilde{\mathbb{E}}$ and $\mathbb{E}\preceq \widetilde{\mathbb{E}}$. The type of an experiment is the totality of all experiments which are equivalent to the given experiment.
Proposition 2.
Let $\mathbb{E}$ and $\widetilde{\mathbb{E}}$ be binary experiments. The following statements are equivalent:
Corollary 3.
Let $\mathbb{E}$ and $\widetilde{\mathbb{E}}$ be binary experiments. The following statements are equivalent:
Proposition 3.
-
(i) The mapping $\mathbb{E}\rightsquigarrow \mathsf{r}_{\mathbb{E}}$ is onto the set of all convex continuous decreasing functions $\mathsf{r}:[0,\hspace{0.1667em}1]\to [0,\hspace{0.1667em}1]$ such that $\mathsf{r}(1)=0$.
-
(ii) The mapping $\mathbb{E}\rightsquigarrow \mathsf{b}_{\mathbb{E}}$ is onto the set of all concave functions $\mathsf{b}:[0,\hspace{0.1667em}1]\to [0,\hspace{0.1667em}1]$ such that $\mathsf{b}(\pi )\le \pi \wedge (1-\pi )$.
-
(iii) The mapping $\mathbb{E}\rightsquigarrow \mu _{\mathbb{E}}$ is onto the set of all probability measures μ on $(\mathbb{R}_{+},\hspace{0.1667em}\mathcal{B}(\mathbb{R}_{+}))$ such that $\int x\hspace{0.1667em}\mu (dx)\le 1$.
Proof.
(i) Let $\mathsf{r}(u)$, $u\in [0,\hspace{0.1667em}1]$, be a convex continuous decreasing function with $\mathsf{r}(1)=0$ and $\mathsf{r}(0)\le 1$. Let $\varOmega =[0,\hspace{0.1667em}1]$ and $\mathcal{F}$ be the Borel σ-field. Define $\mathsf{P}$ on $(\varOmega ,\hspace{0.1667em}\mathcal{F})$ as the Lebesgue measure and ${\mathsf{P}^{\prime }}$ as the measure with the distribution function
Then $Z(u)={F^{\prime }_{-}}(u)$ $\mathsf{P}$-a.s. As in the proof of Theorem 4, it follows that $\mathsf{r}(1-u)=\mathsf{K}_{Z}(u)$. Proposition 1 allows us to conclude that $\mathsf{r}_{\mathbb{E}}=\mathsf{r}$.
(28)
\[ F(x)=\left\{\begin{array}{l@{\hskip10.0pt}l}0,& \text{if}\hspace{2.5pt}x<0,\\{} \mathsf{r}(1-x),& \text{if}\hspace{2.5pt}0\le x<1,\\{} 1,& \text{if}\hspace{2.5pt}x\ge 1.\end{array}\right.\](iii) First, it is evident that $\mu _{\mathbb{E}}$ is a probability measure on $(\mathbb{R}_{+},\hspace{0.1667em}\mathcal{B}(\mathbb{R}_{+}))$ such that $\int x\hspace{0.1667em}\mu _{\mathbb{E}}(dx)\le 1$ for any dichotomy $\mathbb{E}$. Now, let μ be a probability measure on $(\mathbb{R}_{+},\hspace{0.1667em}\mathcal{B}(\mathbb{R}_{+}))$ such that $\int x\hspace{0.1667em}\mu (dx)\le 1$. Put $\varOmega =[0,+\infty ]$ and let $\mathcal{F}$ be the Borel σ-field. Define $\mathsf{P}$ as the probability measure which coincides with μ on Borel subsets of $\mathbb{R}_{+}$. Finally, define ${\mathsf{P}^{\prime }}$ by
\[ {\mathsf{P}^{\prime }}(B\cap \mathbb{R}_{+}):=\int _{B\cap \mathbb{R}_{+}}x\hspace{0.1667em}\mu (dx),\hspace{2em}{\mathsf{P}^{\prime }}\big(\{+\infty \}\big):=1-\int _{\mathbb{R}_{+}}x\hspace{0.1667em}\mu (dx)\text{.}\]
If $\mathbb{E}$ is defined as $\mathbb{E}=(\varOmega ,\hspace{0.1667em}\mathcal{F},\hspace{0.1667em}\mathsf{P},\hspace{0.1667em}{\mathsf{P}^{\prime }})$, it is clear that $\mu _{\mathbb{E}}=\mu $.(ii) First, it follows from the definition of the error function that $0\le \mathsf{b}_{\mathbb{E}}(\pi )\le \pi \wedge (1-\pi )$, $\pi \in [0,\hspace{0.1667em}1]$, and that $\mathsf{b}_{\mathbb{E}}$ is concave. If $\mathsf{b}$ is a function with these properties, then define $\mathsf{J}(x):=x-(1+x)\mathsf{b}(\frac{1}{1+x})$, $x\ge 0$, cf. (26); put also $\mathsf{J}(x)=0$ for $x<0$. Using concavity of $\mathsf{b}$, it is easy to check that $\mathsf{J}$ is convex on $\mathbb{R}_{+}$. Since $\mathsf{b}(0)=0$, we have $\lim _{x\to +\infty }\frac{\mathsf{J}(x)}{x}=1$. The inequalities $0\le \mathsf{b}(\pi )\le 1-\pi $ imply that $0\le \mathsf{J}(x)\le x$ for all $x\ge 0$. In particular, $\mathsf{J}$ is convex on $\mathbb{R}$ and, by Theorem 2, $\mathsf{J}$ is the integrated distribution function of some nonnegative random variable Z. Finally, the inequality $\mathsf{b}(\pi )\le \pi $ implies that $\mathsf{J}(x)\ge x-1$, which means that $\mathsf{E}[Z]\le 1$ by Theorem 1. Hence, $\mathsf{b}$ is the error function of an experiment $\mathbb{E}$ such that $\mu _{\mathbb{E}}=\operatorname{Law}(Z)$. □
Let us note that the proofs of (i) and (iii) give more than it is stated. Starting with a function $\mathsf{r}$ or a measure μ from corresponding classes, we construct an experiment such that its risk function (resp., the distribution of the likelihood ratio) coincides with $\mathsf{r}$ (resp. μ). Now, if we start in (i) with the risk function $\mathsf{r}_{\mathbb{E}}$ of an experiment $\mathbb{E}$, we obtain a new experiment, say, $\varkappa (\mathbb{E})$, equivalent to $\mathbb{E}$. Moreover, experiments $\mathbb{E}_{1}$ and $\mathbb{E}_{2}$ are equivalent if and only if $\varkappa (\mathbb{E}_{1})=\varkappa (\mathbb{E}_{2})$. In other words, the rule $\mathbb{E}\rightsquigarrow \varkappa (\mathbb{E})$ is a representation of binary experiments. Another representation is given in the proof of (iii).
Definition 4.
Let $\mathbb{E}=(\varOmega ,\mathcal{F},\mathsf{P},{\mathsf{P}^{\prime }})$ and $\widetilde{\mathbb{E}}=(\widetilde{\varOmega },\widetilde{\mathcal{F}},\widetilde{\mathsf{P}},{\widetilde{\mathsf{P}}^{\prime }})$ be two binary experiments. $\mathbb{E}$ is called ε-deficient with respect to $\widetilde{\mathbb{E}}$ if for any $\widetilde{\varphi }\in \varPhi (\widetilde{\mathbb{E}})$ there is $\varphi \in \varPhi (\mathbb{E})$ such that $\alpha (\varphi )\le \alpha (\widetilde{\varphi })+\varepsilon /2$ and $\beta (\varphi )\le \beta (\widetilde{\varphi })+\varepsilon /2$. The number
\[ \delta _{2}(\mathbb{E},\hspace{0.1667em}\widetilde{\mathbb{E}}):=\inf \hspace{0.1667em}\{\varepsilon \ge 0:\mathbb{E}\hspace{2.5pt}\text{is}\hspace{2.5pt}\varepsilon \text{-deficient with respect to}\hspace{2.5pt}\widetilde{\mathbb{E}}\}\]
is called the (asymmetric) deficiency of $\mathbb{E}$ with respect to $\widetilde{\mathbb{E}}$. Define also the (symmetric) deficiency
\[ \Delta _{2}(\mathbb{E},\hspace{0.1667em}\widetilde{\mathbb{E}}):=\max \hspace{0.1667em}\big(\delta _{2}(\mathbb{E},\hspace{0.1667em}\widetilde{\mathbb{E}}),\hspace{0.1667em}\delta _{2}(\widetilde{\mathbb{E}},\hspace{0.1667em}\mathbb{E})\big)\]
between $\mathbb{E}$ and $\widetilde{\mathbb{E}}$.It is easy to check that $\mathbb{E}\succeq \widetilde{\mathbb{E}}$ if and only if $\delta _{2}(\mathbb{E},\hspace{0.1667em}\widetilde{\mathbb{E}})=0$. Hence, $\mathbb{E}\sim \widetilde{\mathbb{E}}$ if and only if $\Delta _{2}(\mathbb{E},\hspace{0.1667em}\widetilde{\mathbb{E}})=0$. It is also easy to check that $\delta _{2}$ and $\Delta _{2}$ satisfy the triangle inequality and, hence, $\Delta _{2}$ is a metric on the space of types of experiments. We shall see after the next proposition that this metric space is a compact space.
Proposition 4.
Proof.
(i)$\hspace{0.2778em}\Leftrightarrow \hspace{0.2778em}$(ii) follows immediately from Definition 4, so our goal is to prove (ii)$\hspace{0.2778em}\Leftrightarrow \hspace{0.2778em}$(iii) using dual relations (13) and (14). A direct proof of (i)$\hspace{0.2778em}\Leftrightarrow \hspace{0.2778em}$(iii) can be found in [27].
To simplify the notation, put $\mathsf{K}:=\mathsf{K}_{Z}$, $\mathsf{J}:=\mathsf{J}_{Z}$, while the corresponding functions in the experiment $\widetilde{\mathbb{E}}$ are denoted by $\widetilde{\mathsf{K}}$ and $\widetilde{\mathsf{J}}$. Since $\mathsf{r}_{\mathbb{E}}(u)=\mathsf{K}(1-u)$ (29) is equivalent to
In turn, if follows from (26) that (30) is equivalent to
(31)
\[ \mathsf{K}(u)\le \widetilde{\mathsf{K}}\bigg(u+\frac{\varepsilon }{2}\bigg)+\frac{\varepsilon }{2}\hspace{1em}\text{for all}\hspace{2.5pt}u\in \bigg[0,\hspace{0.1667em}1-\frac{\varepsilon }{2}\bigg].\]Since $\mathsf{J}(x)=0$ for $x\le 0$, we have $\mathsf{K}(u)=\sup _{x\ge 0}\{xu-\mathsf{J}(x)\}$ and similarly for $\widetilde{\mathsf{K}}$. Thus, it follows from (32) that, for $u\ge 0$,
Conversely, let (31) hold true, and let $x>0$ be such that $F_{\widetilde{Z}}(x-0)\ge \frac{\varepsilon }{2}$, where $\widetilde{Z}$ is the Radon–Nikodým derivative of the $\widetilde{\mathsf{P}}$-absolutely continuous part of ${\widetilde{\mathsf{P}}^{\prime }}$ with respect to $\widetilde{\mathsf{P}}$. Then
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \mathsf{J}(x)& \displaystyle \ge \underset{u\in [0,\hspace{0.1667em}1]}{\sup }\big\{xu-\mathsf{K}(u)\big\}\ge \underset{u\in [0,\hspace{0.1667em}1-\frac{\varepsilon }{2}]}{\sup }\big\{xu-\mathsf{K}(u)\big\}\\{} & \displaystyle \ge \underset{u\in [0,\hspace{0.1667em}1-\frac{\varepsilon }{2}]}{\sup }\bigg\{xu-\frac{\varepsilon }{2}-\widetilde{\mathsf{K}}\bigg(u+\frac{\varepsilon }{2}\bigg)\bigg\}=\underset{u\in [\frac{\varepsilon }{2},\hspace{0.1667em}1]}{\sup }\bigg\{xu-\frac{(1+x)\varepsilon }{2}-\widetilde{\mathsf{K}}(u)\bigg\}\\{} & \displaystyle =-\frac{\varepsilon }{2}(x+1)+\widetilde{\mathsf{J}}(x)\text{,}\end{array}\]
where the last equality follows from the fact that the supremum in (14) is attained at $u\in [F_{\widetilde{Z}}(x-0),\hspace{0.1667em}F_{\widetilde{Z}}(x)]$, cf. (17). It remains to note that if x is such that $F_{\widetilde{Z}}(x-0)<\frac{\varepsilon }{2}$, then $\widetilde{\mathsf{J}}(x)\le \frac{\varepsilon x}{2}$ and (32) is obviously true. □As a consequence, we obtain the following expressions for $\delta _{2}(\mathbb{E},\hspace{0.1667em}\widetilde{\mathbb{E}})$ and $\Delta _{2}(\mathbb{E},\hspace{0.1667em}\widetilde{\mathbb{E}})$, see ([27], [28, p. 604]):
Corollary 4.
Let $\mathbb{E}$ and $\widetilde{\mathbb{E}}$ be binary experiments. Then
\[\begin{array}{r@{\hskip0pt}l}\displaystyle \delta _{2}(\mathbb{E},\hspace{0.1667em}\widetilde{\mathbb{E}})& \displaystyle =\frac{1}{2}\underset{\pi \in [0,\hspace{0.1667em}1]}{\sup }\big\{\mathsf{b}_{\mathbb{E}}(\pi )-\mathsf{b}_{\widetilde{\mathbb{E}}}(\pi )\big\},\\{} \displaystyle \Delta _{2}(\mathbb{E},\hspace{0.1667em}\widetilde{\mathbb{E}})& \displaystyle =\frac{1}{2}\underset{\pi \in [0,\hspace{0.1667em}1]}{\sup }\big|\mathsf{b}_{\mathbb{E}}(\pi )-\mathsf{b}_{\widetilde{\mathbb{E}}}(\pi )\big|=\frac{1}{2}L(F,\widetilde{F}),\end{array}\]
where $L(\cdot ,\cdot )$ is the Lévy distance between distribution functions, F is defined as in (28) with $\mathsf{r}=\mathsf{r}_{\mathbb{E}}$, and $\widetilde{F}$ is defined similarly with $\mathsf{r}=\mathsf{r}_{\widetilde{\mathbb{E}}}$.
The subset of concave functions $\mathsf{b}$ on $[0,\hspace{0.1667em}1]$ satisfying $0\le \mathsf{b}(\pi )\le \pi \wedge (1-\pi )$ is clearly closed with respect to uniform convergence and is equicontinuous. By the Arzela–Ascoli theorem, this subset is a compact in the space $C[0,\hspace{0.1667em}1]$ with sup-norm. Therefore, the space of types of experiments is a compact metric space with $\Delta _{2}$-metric.
Definition 5.
Let $\mathbb{E}=(\varOmega ,\mathcal{F},\mathsf{P},{\mathsf{P}^{\prime }})$ and ${\mathbb{E}}^{n}=({\varOmega }^{n},{\mathcal{F}}^{n},{\mathsf{P}}^{n},{\mathsf{P}^{\prime n}})$, $n\ge 1$, be binary experiments. We say that ${\mathbb{E}}^{n}$ weakly converges to $\mathbb{E}$ if $\Delta _{2}({\mathbb{E}}^{n},\hspace{0.1667em}\mathbb{E})\to 0$ as $n\to \infty $.
Proposition 5.
Let $\mathbb{E}$ and ${\mathbb{E}}^{n}$, $n\ge 1$, be binary experiments. The following statements are equivalent:
-
(i) $\Delta _{2}({\mathbb{E}}^{n},\hspace{0.1667em}\mathbb{E})\to 0$.
-
(ii) $\mathsf{r}_{{\mathbb{E}}^{n}}$ converges to $\mathsf{r}_{\mathbb{E}}$ pointwise on $(0,\hspace{0.1667em}1]$.
-
(ii′) $\mathsf{r}_{{\mathbb{E}}^{n}}$ converges uniformly to $\mathsf{r}_{\mathbb{E}}$ on any $[a,\hspace{0.1667em}1]\subset (0,\hspace{0.1667em}1]$.
-
(iii) $\mathsf{b}_{{\mathbb{E}}^{n}}$ converges uniformly to $\mathsf{r}_{\mathbb{E}}$ on $[0,\hspace{0.1667em}1]$.
-
(iv) $\mu _{{\mathbb{E}}^{n}}$ weakly converges to $\mu _{\mathbb{E}}$.
Proof.
The equivalences (i)$\hspace{0.2778em}\Leftrightarrow \hspace{0.2778em}$(ii) and (i)$\hspace{0.2778em}\Leftrightarrow \hspace{0.2778em}$(iii) follow from Corollary 4, and the equivalence of (ii), (ii′), and (iv) is a consequence of Theorem 10 and Proposition 1. However, we prefer to give a direct proof of the equivalence (i)$\hspace{0.2778em}\Leftrightarrow \hspace{0.2778em}$(ii) without using the Lévy distance.
Assume (i). By (29),
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \mathsf{r}_{{\mathbb{E}}^{n}}(u)+\frac{\Delta _{2}({\mathbb{E}}^{n},\hspace{0.1667em}\mathbb{E})}{2}\ge \mathsf{r}_{\mathbb{E}}\bigg(u+\frac{\Delta _{2}({\mathbb{E}}^{n},\hspace{0.1667em}\mathbb{E})}{2}\bigg),\hspace{2em}0\le u\le 1-\frac{\Delta _{2}({\mathbb{E}}^{n},\hspace{0.1667em}\mathbb{E})}{2},\\{} & \displaystyle \mathsf{r}_{\mathbb{E}}\bigg(u-\frac{\Delta _{2}({\mathbb{E}}^{n},\hspace{0.1667em}\mathbb{E})}{2}\bigg)+\frac{\Delta _{2}({\mathbb{E}}^{n},\hspace{0.1667em}\mathbb{E})}{2}\ge \mathsf{r}_{{\mathbb{E}}^{n}}(u),\hspace{2em}\frac{\Delta _{2}({\mathbb{E}}^{n},\hspace{0.1667em}\mathbb{E})}{2}\le u\le 1.\end{array}\]
Passing to the limit as $n\to \infty $, we get
\[\begin{array}{r@{\hskip0pt}l}& \displaystyle \underset{n\to \infty }{\liminf }\mathsf{r}_{{\mathbb{E}}^{n}}(u)\ge \mathsf{r}_{\mathbb{E}}(u)\hspace{1em}\text{for}\hspace{2.5pt}0\le u<1,\\{} & \displaystyle \mathsf{r}_{\mathbb{E}}(u)\ge \underset{n\to \infty }{\limsup }\mathsf{r}_{{\mathbb{E}}^{n}}(u)\hspace{1em}\text{for}\hspace{2.5pt}0<u\le 1.\end{array}\]
Combining these inequalities, we obtain $\lim _{n\to \infty }\mathsf{r}_{{\mathbb{E}}^{n}}(u)=\mathsf{r}_{\mathbb{E}}(u)$ for $0<u<1$. Since risk functions vanish at 1, the convergence holds for $u=1$ as well.Now the converse implication (ii)$\hspace{0.2778em}\Rightarrow \hspace{0.2778em}$(i) is proved by standard compactness arguments. □
5 Chacon–Walsh revisited
The Skorokhod embedding problem was posed and solved by Skorokhod [26] in the following form: given a centered distribution μ with finite second moment, find a stopping time T such that $\mathsf{E}[T]<\infty $ and $\operatorname{Law}(B_{T})=\mu $, where $B=(B_{t})_{t\ge 0}$, $B_{0}=0$, is a standard Brownian motion. Chacon and Walsh [4] suggest to construct T as the limit of an increasing sequence of stopping times $T_{n}$, each being the first exit time (after the previous one) of B from a compact interval. This construction has a simple graphical interpretation in terms of the potential functions of $B_{T_{n}}$ (we recall that potential functions are defined in (3)).
Cox [6] extends the Chacon–Walsh construction to a more general case. He considers a Brownian motion $B=(B_{t})_{t\ge 0}$ with a given integrable starting distribution $\mu _{0}$ for $B_{0}$ and a general integrable target distribution μ. A solution T (such that $\operatorname{Law}(B_{T})=\mu $) must be found in the class of minimal stopping times.
It is easy to observe that the Chacon–Walsh construction has a graphical interpretation in terms of integrated quantile functions as well; moreover, in our opinion, the picture is more simple. We give alternative proofs of the result in [4] and of some results in [6]. Moreover, we construct a minimal stopping time in some special case where $\mu _{0}$ and μ may be non-integrable.
Let us recall the definition of the balayage. For a probability measure μ on $\mathbb{R}$ and an interval $I=(a,\hspace{0.1667em}b)$, $-\infty <a<b<+\infty $, the balayage $\mu _{I}$ of μ on I is defined as the measure which coincides with μ outside $[a,\hspace{0.1667em}b]$, vanishes on $(a,\hspace{0.1667em}b)$, and such that
Since
the balayage $\mu _{I}$ is a probability measure and has the same mean as μ (if defined). It follows that, if $B=(B_{t})_{t\ge 0}$ is a continuous local martingale with $\langle B,B\rangle _{\infty }=\infty $ a.s. (e. g. a Brownian motion), μ is the distribution of $B_{S}$, where S is a stopping time, and the stopping time T is defined by
then $T<+\infty $ a. s. and the distribution of $B_{T}$ is the balayage $\mu _{I}$.
(33)
\[ \mu _{I}\big(\{a\}\big)=\int _{[a,\hspace{0.1667em}b]}\frac{b-x}{b-a}\hspace{0.1667em}\mu (dx),\hspace{2em}\mu _{I}\big(\{b\}\big)=\int _{[a,\hspace{0.1667em}b]}\frac{x-a}{b-a}\hspace{0.1667em}\mu (dx)\text{.}\](34)
\[ \int _{[a,\hspace{0.1667em}b]}\mu _{I}(dx)=\int _{[a,\hspace{0.1667em}b]}\mu (dx)\hspace{1em}\text{and}\hspace{1em}\int _{[a,\hspace{0.1667em}b]}x\hspace{0.1667em}\mu _{I}(dx)=\int _{[a,\hspace{0.1667em}b]}x\hspace{0.1667em}\mu (dx),\]Let X and Y be random variables with the distributions μ and $\mu _{I}$ respectively. It is clear that
\[ {q_{Y}^{L}}(u)=\left\{\begin{array}{l@{\hskip10.0pt}l}{q_{X}^{L}}(u),& \text{if}\hspace{2.5pt}0<u\le F_{X}(a-0)\hspace{2.5pt}\text{or}\hspace{2.5pt}F_{X}(b)<u<1,\\{} a,& \text{if}\hspace{2.5pt}F_{X}(a-0)<u\le F_{X}(a-0)+\mu _{I}(\{a\}),\\{} b,& \text{if}\hspace{2.5pt}F_{X}(a-0)+\mu _{I}(\{a\})<u\le F_{X}(b).\end{array}\right.\]
Moreover, the second equality in (34) can be rewritten as
\[ \mathsf{K}_{X}\big(F_{X}(b)\big)-\mathsf{K}_{X}\big(F_{X}(a-0)\big)=\mathsf{K}_{X}\big(F_{Y}(b)\big)-\mathsf{K}_{X}\big(F_{Y}(a-0)\big)\text{.}\]
This allows us to describe how to obtain the integrated quantile function of Y: pass the tangent lines with the slopes a and b to the graph of $\mathsf{K}_{X}$, replace the curve on this graph between points where the graph meets the lines by the corresponding segments of these lines. If the point of intersection of these lines lies below the horizontal axis, then shift the resulting graph vertically upwards so that this point will come on the horizontal axis.Fig. 6.
Graphs of shifted integrated quantile functions ${\mathsf{K}_{X}^{[1]}}$ and ${\mathsf{K}_{Y}^{[1]}}$: the distribution of Y is the balayage of the distribution of X
If $\mathsf{E}[{X}^{+}]<\infty $ (resp. $\mathsf{E}[{X}^{-}]<\infty $), then $\mathsf{E}[{Y}^{+}]<\infty $ (resp. $\mathsf{E}[{Y}^{-}]<\infty $), and the last step is not needed if we deal with shifted integrated quantile functions ${\mathsf{K}_{X}^{[1]}}$ and ${\mathsf{K}_{Y}^{[1]}}$ (resp. ${\mathsf{K}_{X}^{[0]}}$ and ${\mathsf{K}_{Y}^{[0]}}$), see Fig. 6. We state this fact in the following lemma only in the case where $\mathsf{E}[{X}^{+}]<\infty $. Its proof is immediate from the previous paragraph.
Lemma 1.
Let μ be the distribution of a random variable X with $\mathsf{E}[{X}^{+}]<\infty $, $\operatorname{Law}(Y)=\mu _{I}$, where $I=(a,\hspace{0.1667em}b)$ is a finite interval. Put $u_{a}:=F_{X}(a-0)$ and $u_{b}:=F_{X}(b)$. Then $\mathsf{E}[{Y}^{+}]<\infty $ and
\[ {\mathsf{K}_{Y}^{[1]}}(u)=\left\{\begin{array}{l@{\hskip10.0pt}l}{\mathsf{K}_{X}^{[1]}}(u),& \textit{if}\hspace{2.5pt}u\notin (u_{a},\hspace{0.1667em}u_{b}),\\{} \big(a(u-u_{a})+{\mathsf{K}_{X}^{[1]}}(u_{a})\big)\vee \big(b(u-u_{b})+{\mathsf{K}_{X}^{[1]}}(u_{b})\big),& \textit{if}\hspace{2.5pt}u\in (u_{a},\hspace{0.1667em}u_{b}).\end{array}\right.\]
In particular, ${\mathsf{K}_{Y}^{[1]}}(u)\le {\mathsf{K}_{X}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$.
The next lemma is a key tool in our future construction.
Lemma 2.
Let X and Y be random variables such that $\mathsf{E}[{X}^{+}]<\infty $, $\mathsf{E}[{Y}^{+}]<\infty $, and ${\mathsf{K}_{Y}^{[1]}}(u)\le {\mathsf{K}_{X}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$. Fix $v\in (0,\hspace{0.1667em}1)$. Then there is a random variable Z such that ${\mathsf{K}_{Y}^{[1]}}(u)\le {\mathsf{K}_{Z}^{[1]}}(u)\le {\mathsf{K}_{X}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$, ${\mathsf{K}_{Z}^{[1]}}(v)={\mathsf{K}_{Y}^{[1]}}(v)$, and the distribution of Z is a balayage of the distribution of X.
Proof.
Without loss of generality, we may assume that ${\mathsf{K}_{X}^{[1]}}(v)>{\mathsf{K}_{Y}^{[1]}}(v)$. Let us consider the following equation:
The maximum of the left-hand side over x equals $\mathsf{K}_{X}(v)-\mathsf{E}[{X}^{+}]={\mathsf{K}_{X}^{[1]}}(v)$ and is greater than the right-hand side. Moreover, it is attained at $x\in [{q_{X}^{L}}(v),\hspace{0.1667em}{q_{X}^{R}}(v)]$. Further, applying Theorem 1 (iv)–(v), we get
\[ \underset{x\to +\infty }{\lim }\big(xv-\mathsf{J}_{X}(x)\big)=\underset{x\to +\infty }{\lim }\big(x-\mathsf{J}_{X}(x)\big)+\underset{x\to +\infty }{\lim }(v-1)x=-\infty \]
and
\[ \underset{x\to -\infty }{\lim }\big(xv-\mathsf{J}_{X}(x)\big)=\underset{x\to -\infty }{\lim }x\bigg(v-\frac{\mathsf{J}_{X}(x)}{x}\bigg)=-\infty \text{.}\]
Since the left-hand side of (36) is a concave function in x, the equation (36) has two solutions $a<{q_{X}^{L}}(v)$ and $b>{q_{X}^{R}}(v)$, i. e. $F_{X}(a)<v<F_{X}(b-0)$.Using Corollary 2, rewrite equation (36) in the form
\[ {\mathsf{K}_{X}^{[1]}}\big(F_{X}(x)\big)={\mathsf{K}_{Y}^{[1]}}(v)+x\big(F_{X}(x)-v\big)\text{.}\]
This equality for $x=a$ (resp. $x=b$) says that the straight line with the slope a (resp. b) and passing through the point $(v,\hspace{0.1667em}{\mathsf{K}_{Y}^{[1]}}(v))$ meets the curve ${\mathsf{K}_{X}^{[1]}}$ at the point where the first coordinate is $F_{X}(a)$ (resp. $F_{X}(b)$). Due to (17), these straight lines are tangent lines to the curve ${\mathsf{K}_{X}^{[1]}}$. Comparing with Lemma 1, we obtain that a random variable Z such that its distribution is the balayage of the distribution of X on $I=(a,\hspace{0.1667em}b)$ satisfies all the requirements. □From now on, we assume that there is a probability space with filtration $(\varOmega ,\mathcal{F},(\mathcal{F}_{t})_{t\ge 0},\mathsf{P})$ and an $(\mathcal{F}_{t},\mathsf{P})$-Brownian motion $B=(B_{t})_{t\ge 0}$ with an arbitrary initial distribution. For $c>0$, let
The next lemma is inspired by Theorem 5 in [7].
Lemma 3.
Let S be a stopping time and T defined by (35) with $I=(a,b)$. If $\mathsf{E}[{B_{S}^{+}}]<\infty $ and $c\mathsf{P}(S\ge H_{c})\le \mathsf{E}[B_{S}\mathbb{1}_{\{S\ge H_{c}\}}]$, then $\mathsf{E}[{B_{T}^{+}}]<\infty $ and $c\mathsf{P}(T\ge H_{c})\le \mathsf{E}[B_{T}\mathbb{1}_{\{T\ge H_{c}\}}]$.
Proof.
By the strong Markov property, in view of boundedness of the random variables under the conditional expectations below,
\[ \mathsf{E}[B_{T}-B_{S}|\mathcal{F}_{S}]=0\hspace{1em}\text{and}\hspace{1em}\mathsf{E}[B_{T}-B_{(S\vee H_{c})\wedge T}|\mathcal{F}_{(S\vee H_{c})\wedge T}]=0.\]
Since $\{S\ge H_{c}\}\in \mathcal{F}_{S}$ and $\{S<H_{c}\le T\}\in \mathcal{F}_{(S\vee H_{c})\wedge T}$, we get
\[\begin{array}{r@{\hskip0pt}l}\displaystyle c\mathsf{P}(T\ge H_{c})& \displaystyle =c\mathsf{P}(S\ge H_{c})+c\mathsf{P}(T\ge H_{c}>S)\\{} & \displaystyle \le \mathsf{E}[B_{S}\mathbb{1}_{\{S\ge H_{c}\}}]+\mathsf{E}[B_{(S\vee H_{c})\wedge T}\mathbb{1}_{\{S<H_{c}\le T\}}]\\{} & \displaystyle =\mathsf{E}[B_{T}\mathbb{1}_{\{S\ge H_{c}\}}]+\mathsf{E}[B_{T}\mathbb{1}_{\{S<H_{c}\le T\}}]=\mathsf{E}[B_{T}\mathbb{1}_{\{T\ge H_{c}\}}].\end{array}\]
□Let us also recall that T is a minimal stopping time if any stopping time $R\le T$ with $\operatorname{Law}(B_{R})=\operatorname{Law}(B_{T})$ satisfies $R=T$ a. s.
Theorem 11.
Let $\mu _{0}$ and μ be distributions on $\mathbb{R}$ such that $\int _{\mathbb{R}}{x}^{+}\hspace{0.1667em}\mu (dx)<\infty $ and
\[ \int _{\mathbb{R}}{(x-y)}^{+}\hspace{0.1667em}\mu _{0}(dx)\le \int _{\mathbb{R}}{(x-y)}^{+}\hspace{0.1667em}\mu (dx)\hspace{1em}\textit{for all}\hspace{2.5pt}y\in \mathbb{R}.\]
Let B be a Brownian motion with the initial distribution $\operatorname{Law}(B_{0})=\mu _{0}$. Then there is an increasing sequence of stopping times $0=T_{0}\le T_{1}\le \cdots \le T_{n}\le \dots \hspace{0.1667em}$ such that $T:=\lim _{n\to \infty }T_{n}$ is a minimal a. s. finite stopping time, the distribution of $B_{T_{n}}$ is a balayage of the distribution of $B_{T_{n-1}}$ for each $n=1,2,\dots \hspace{0.1667em}$, and $\operatorname{Law}(B_{T})=\mu $.
Proof.
Put $X_{0}:=B_{T_{0}}$ and let $\operatorname{Law}(Y)=\mu $. Then ${\mathsf{K}_{Y}^{[1]}}(u)\le {\mathsf{K}_{X_{0}}^{[1]}}(u)$ for all $u\in [0,\hspace{0.1667em}1]$. Take an arbitrary sequence $\{v_{n}\}$ of distinct points in $(0,\hspace{0.1667em}1)$ such that $\{v_{n}:n=1,\hspace{0.1667em}2,\hspace{0.1667em}\dots \hspace{0.1667em}\}$ is dense in $[0,\hspace{0.1667em}1]$. Recursively define $X_{n}$ as Z in Lemma 2 applied to $X=X_{n-1}$, Y, and $v=v_{n}$. Then we obtain a sequence $\{X_{n}\}$ of random variables such that
\[ {\mathsf{K}_{Y}^{[1]}}(u)\le {\mathsf{K}_{X_{n}}^{[1]}}(u)\le {\mathsf{K}_{X_{n-1}}^{[1]}}(u)\le {\mathsf{K}_{X_{0}}^{[1]}}(u),\hspace{1em}u\in (0,\hspace{0.1667em}1],\]
and ${\mathsf{K}_{Y}^{[1]}}(v_{n})={\mathsf{K}_{X_{n}}^{[1]}}(v_{n})$, which implies ${\mathsf{K}_{Y}^{[1]}}(v_{n})={\mathsf{K}_{X_{m}}^{[1]}}(v_{n})$ for all n and $m\ge n$. Then $\lim _{n\to \infty }{\mathsf{K}_{X_{n}}^{[1]}}(u)$ exists, is finite for all $u\in (0,\hspace{0.1667em}1)$, and coincides with ${\mathsf{K}_{Y}^{[1]}}(u)$ on the set $\{v_{n}:n=1,\hspace{0.1667em}2,\hspace{0.1667em}\dots \hspace{0.1667em}\}$. Being a convex function in u, this limit coincides with ${\mathsf{K}_{Y}^{[1]}}(u)$ everywhere on $(0,\hspace{0.1667em}1)$. It follows from Remark 3 that $X_{n}$ weakly converges to Y and the sequence $\{{X_{n}^{+}}\}$ is uniformly integrable.Moreover, the construction in Lemma 2 provides an interval $(a,b)$ denoted by $I_{n}$ such that the distribution of $X_{n}$ is the balayage of the distribution of $X_{n-1}$ on $I_{n}$. Now recursively define
Then $B_{T_{n}}$ has the same distribution as $X_{n}$. Since
\[ \mathsf{E}[B_{0}\mathbb{1}_{\{0\ge H_{c}\}}]=\mathsf{E}[B_{0}\mathbb{1}_{\{B_{0}\ge c\}}]\ge c\mathsf{P}(B_{0}\ge c)\text{,}\]
we conclude from Lemma 3 that, for any $c>0$ and n,
\[ c\mathsf{P}(T_{n}\ge H_{c})\le \mathsf{E}[B_{T_{n}}\mathbb{1}_{\{T_{n}\ge H_{c}\}}]\le \mathsf{E}\big[{B_{T_{n}}^{+}}\big]\le \mathsf{E}\big[{Y}^{+}\big].\]
If $\mathsf{P}(T=\infty )=\delta >0$, then the limit of the expression on the left in the last inequality is greater than or is equal to $c\delta $, which is greater than the right-hand side if c is large enough. This contradiction proves that $T<\infty $ a.s. This implies that $B_{T_{n}}$ converges a.s. to $B_{T}$ and, hence, $\operatorname{Law}(B_{T})=\mu $.It remains to prove that T is a minimal stopping time. According to Theorem 4.1 in [12], it is enough to find a one-to-one function G such that $G{(B)}^{T}$ is a closed submartingale.
Let $g(x)$, $x\in \mathbb{R}$, be a continuously differentiable function with the following properties: $g\equiv 1$ on $[0,+\infty )$ and is strictly positive and increasing on $(-\infty ,0]$, ${\int _{-\infty }^{0}}g(x)\hspace{0.1667em}dx<\infty $, and ${g^{\prime }}(x)\le 1$ for all x. Put $G(y):={\int _{0}^{y}}g(x)\hspace{0.1667em}dx$, then, in particular, G is strictly increasing and bounded from below, and $G(y)=y$ for $y\ge 0$. By Itô’s formula,
\[ G(B_{t})=G(B_{0})+{\int _{0}^{t}}g(B_{s})\hspace{0.1667em}dB_{s}+\frac{1}{2}{\int _{0}^{t}}{g^{\prime }}(s)\hspace{0.1667em}ds=:G(B_{0})+M_{t}+A_{t}\text{,}\]
where $G(B_{0})$ is an integrable random variable, M is a local martingale and $[M,M]_{t}={\int _{0}^{t}}{g}^{2}(B_{s})\hspace{0.1667em}ds\le t$. Hence, by the Burkholder–Davis–Gundy inequality, $\mathsf{E}\sup _{s\le t}|M_{s}|$ is integrable; in particular, M is a martingale. Finally, A is an increasing process and $A_{t}\le t/2$. Therefore, $G(B)$ is a submartingale and, hence, so are the stopped processes $G{(B)}^{T}$ and $G{(B)}^{T_{n}}$. Note that, by construction, the process ${(B-B_{0})}^{T_{n}}$ is bounded (by the sum of the lengths of $I_{k}$, $k\le n$) for a fixed n. Hence, $G(B_{t\wedge T_{n}})\le {B_{t\wedge T_{n}}^{+}}\le {B_{0}^{+}}+\sup _{s\le T_{n}}|B_{s}-B_{0}|$. We conclude that the submartingale $G{(B)}^{T_{n}}$ is uniformly integrable, hence, $G(B_{t\wedge T_{n}})\le _{icx}G(B_{T_{n}})$ for any n and t. On the other hand, ${B_{T_{n}}^{+}}\le _{icx}{B_{T}^{+}}$. Combining, we get ${[G(B_{t\wedge T_{n}})]}^{+}\le _{icx}{B_{T}^{+}}$ for any n and t. We can pass to the limit as $n\to \infty $ in this inequality, which shows that the family ${[G(B_{t\wedge T})]}^{+}$, $t\in \mathbb{R}_{+}$, is uniformly integrable. The claim follows. □Remark 6.
Let $\mu _{0}$ and μ satisfy the assumptions of Theorem 11. As a by-product, we have obtained the following classical characterization of increasing convex order: there exist random variables $X_{0}$ and X defined on the same probability space such that $\operatorname{Law}(X_{0})=\mu _{0}$, $\operatorname{Law}(X)=\mu $ and
Indeed, take $X_{0}=B_{0}$ and $X=B_{T}$ and use the uniform integrability of $({B_{T_{n}}^{+}})_{n\ge 1}$ to obtain the desired inequality.